计算机组成原理数据的表示和运算
进位计数制
- 符号反映权重：罗马数字Ⅴ=5。
- 十进制：数字符号反映权重，且符号位置也反映权重（位权）。
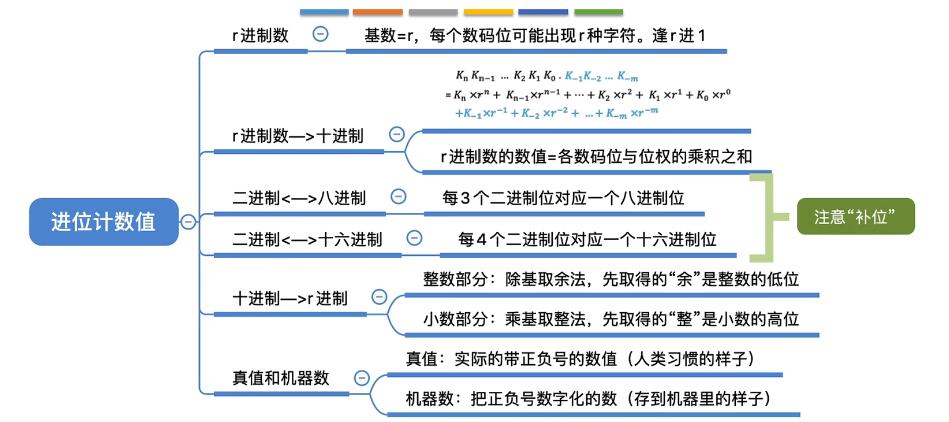
- 进位计数制（逢N进1）：基数（每个数码位所用到的不同符号的个数，r进制的基数为r）。
- 进制之间相互转化：
各进制转化为十进制。
十进制转化为各进制。（整数部分用短除法：不停除r求余数，先得到的余数是低位。小数部分用乘积取整法：不停乘r取整数，先得到的整数是高位）
二进制变为八进制和十六进制。（分别是3或4位变为1位）
十六，八进制转化为二进制。（1位变为4或3位） - 真值：符合人类习惯的数字。
机器数：数字实际存到机器里的形式（正负号需要添加符号位0/1）BCD码
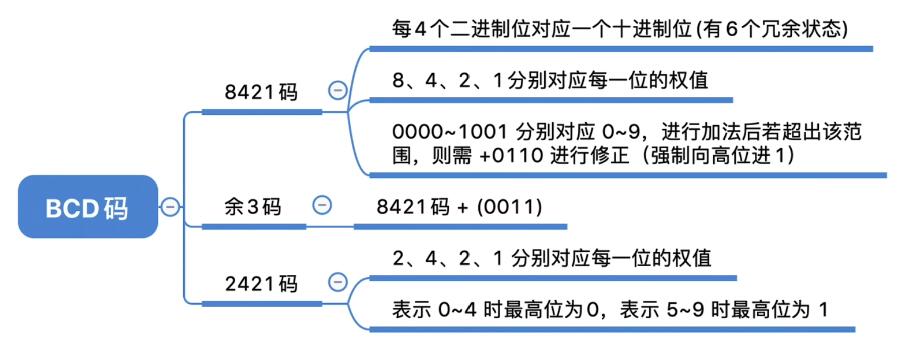
- 8421码：四个位表示一个十进制数字。进行加法运算时若结果位于10-15内，后四位就继续加6（0110），进一位.若结果大于15时，后四位也加6（0110）。————有权码
- 余3码：8421码+（0011）————无权码
- 2421码：改变权值的定义，5以后的数字首位必为1。
字符和字符串
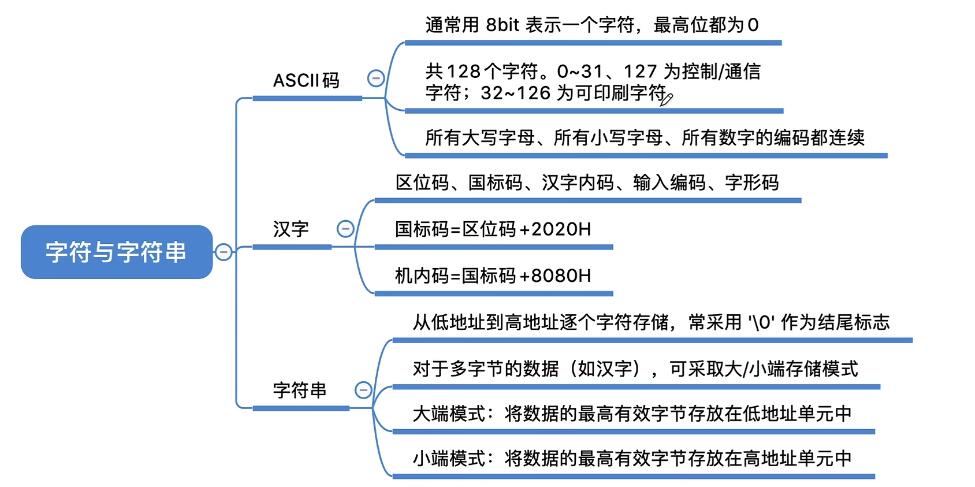
- ASCII码：8位，128个字符（7位即可高位补0），32-126是可打印字符，其余字符是控制和通信字符。
- 汉字的表示和编码：GB2312-80汉字+各种符号共7445个，定义了区位码（94X94个位置）映射到汉字。为了防止信息交互和ASCII码冲突，+20H得到国标码，进一步得到汉字内码。汉字输入输出通过国标码和汉字内码实现二进制和汉字之间转换。
- 字符串：按字节编址，连续存储，最后一位/0。带汉字的时候两个地址存一个汉字。
奇偶校验码
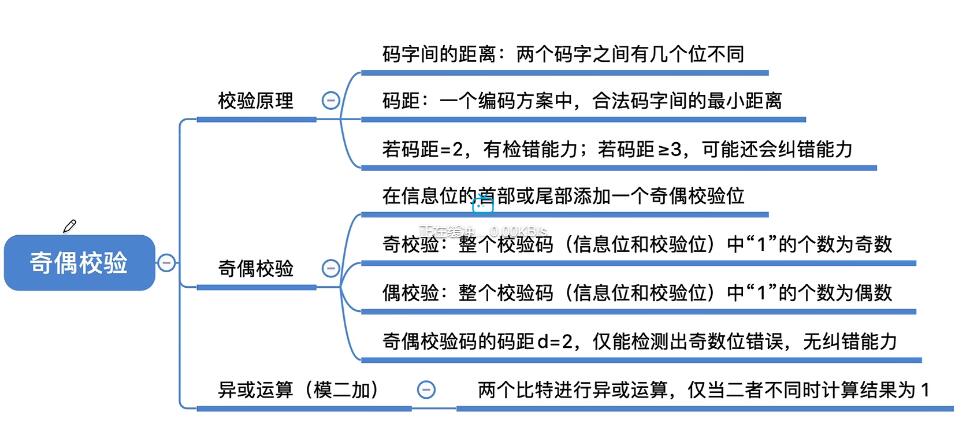位错误导致01反转。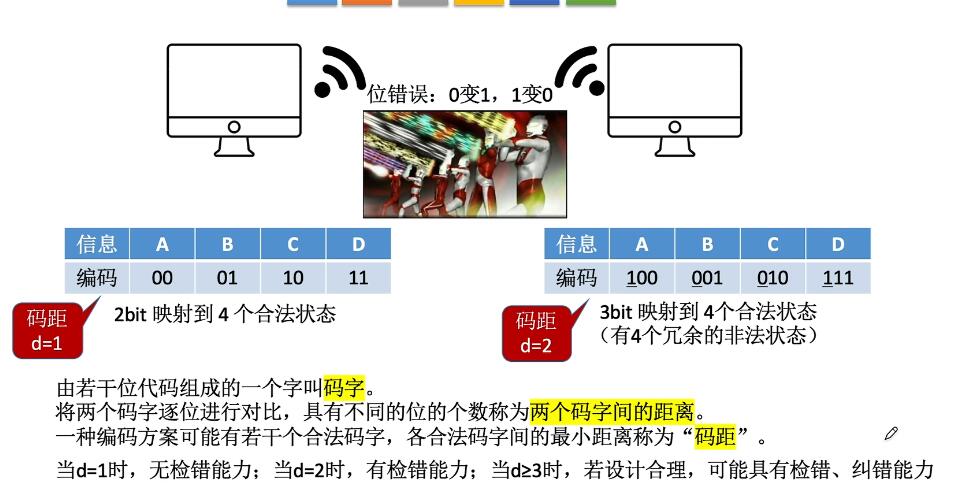
- 添加一个奇偶校验位。
奇校验码：码中1的个数为奇数。
偶校验码：码中1的个数为偶数。但多个位错误有可能检测不出来。 - 求偶校验位：所有位数异或得到。
而进行偶校验时候，则把所有位异或看是否为0，为0则正确否则为错误。海明校验码
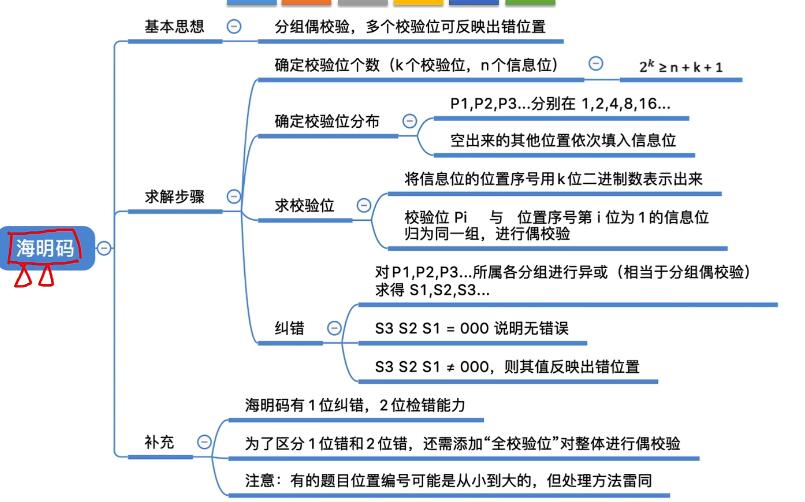奇偶校验码没法查看哪些错误，只能反馈对/错。而海明码则把信息位分组进行偶校验，设置多个校验位，找出出错位置。 - 信息n位，校验k位，则2的k次方大于等于n+k+1。
其中校验位的值根据信息位的位置求得，各个分组异或得到。
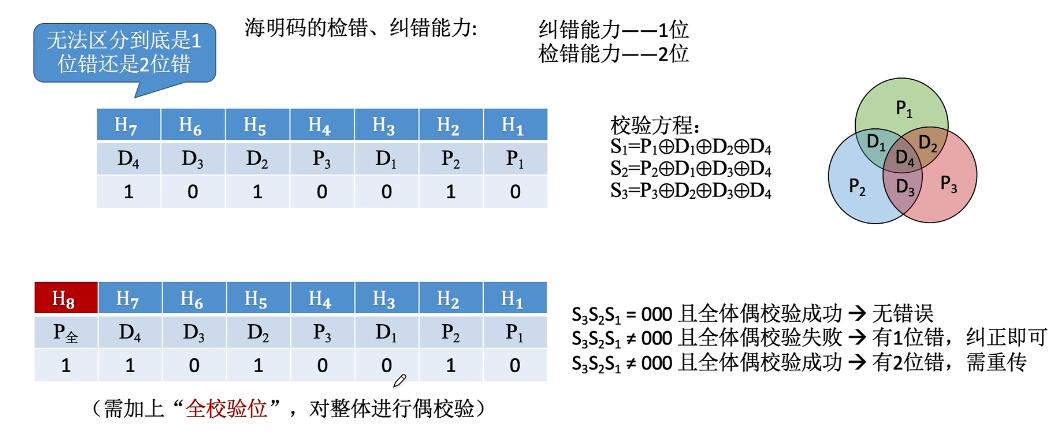
循环冗余校验码
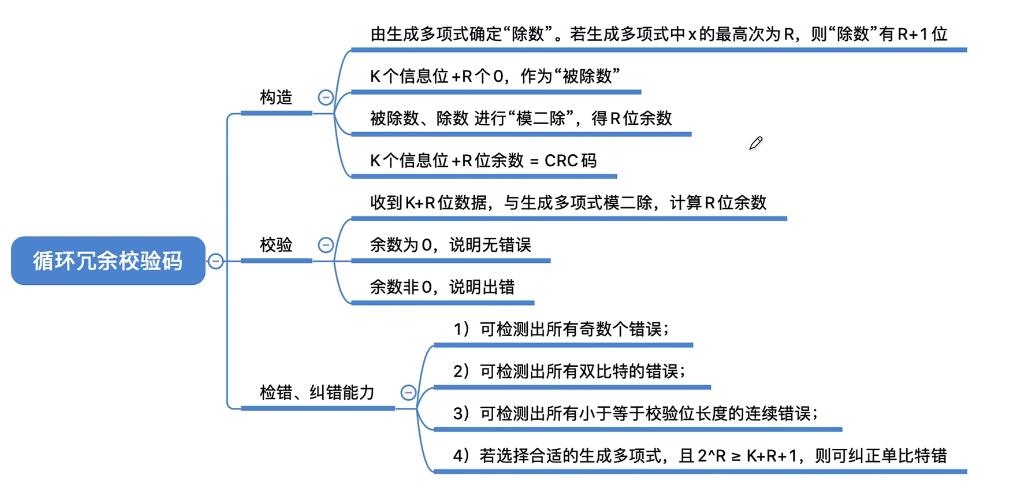
- 数据发送和接收方约定一个“除数”，K信息位+R校验位作为”被除数“,添加校验位之后保证余数为0，接收方检查余数是否为0。非0则重传/单比特纠错。当2的R次方大于等于K+R+1的时候，CRC码可以纠正一位错误（否则位置大于信息位能表示的位个数）
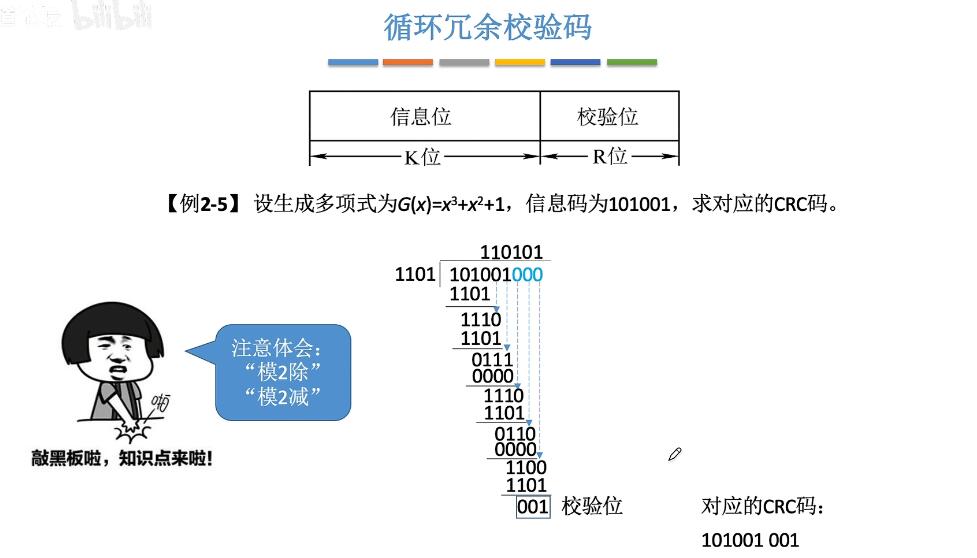
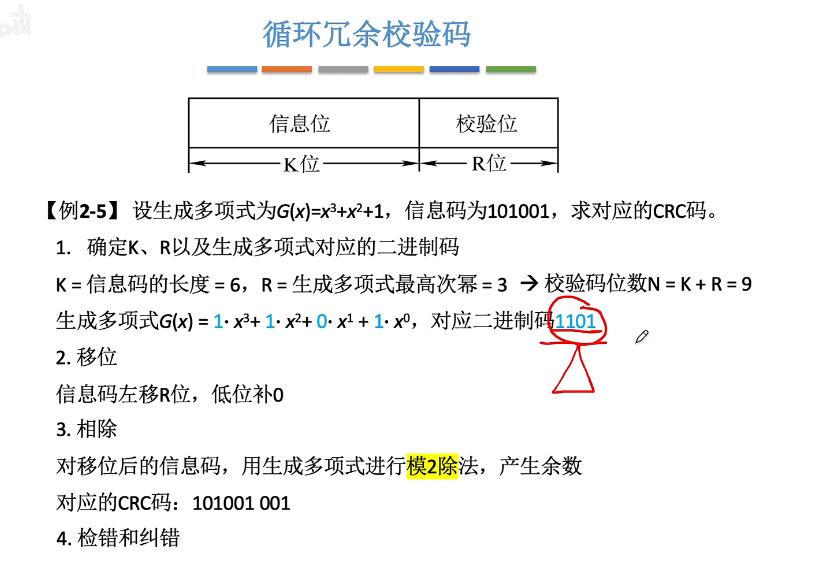
定点数的表示
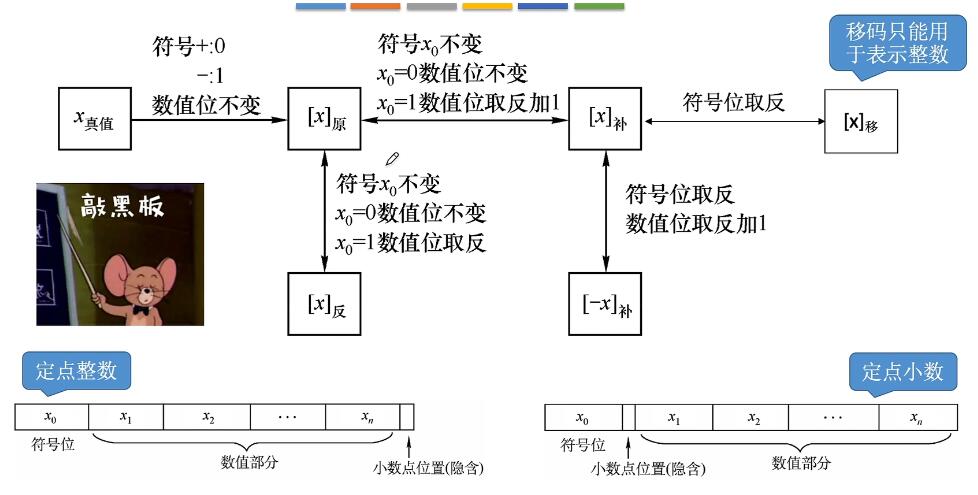定点数：小数点固定，比如99.99。
浮点数：小数点不固定，比如9.999*10（科学计数法） - 无符号数：整个机器字长全部二进制位均为数值位，没有符号位，通常是整数。表示范围0-2的n次方-1。
- 有符号数：分别保存整数和小数
原码：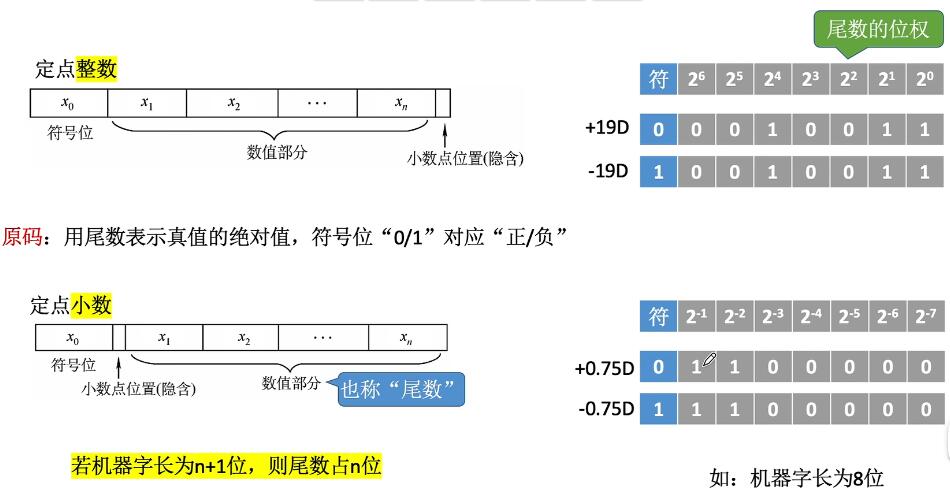
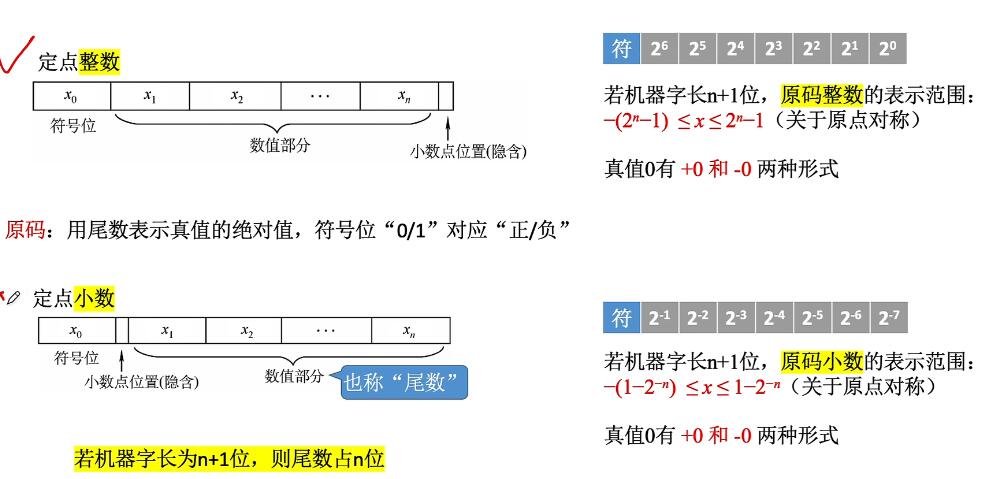反码：
若符号为0，则反码和原码相同，否则数值位全部取反。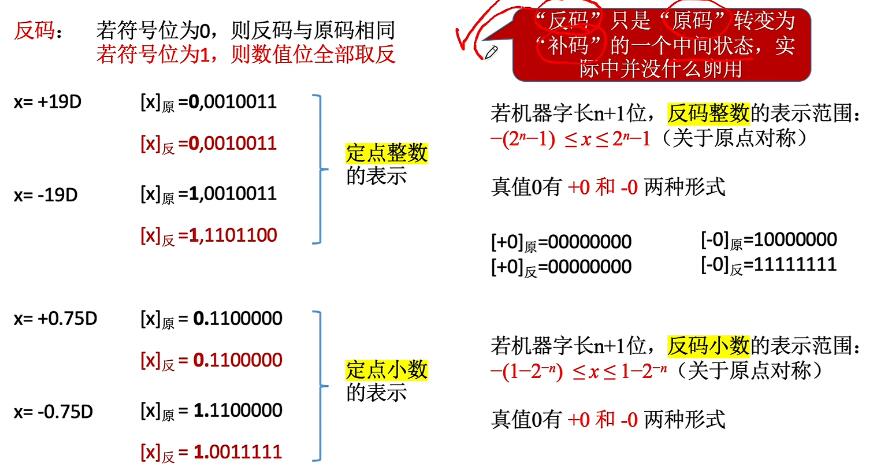
补码： 
移码：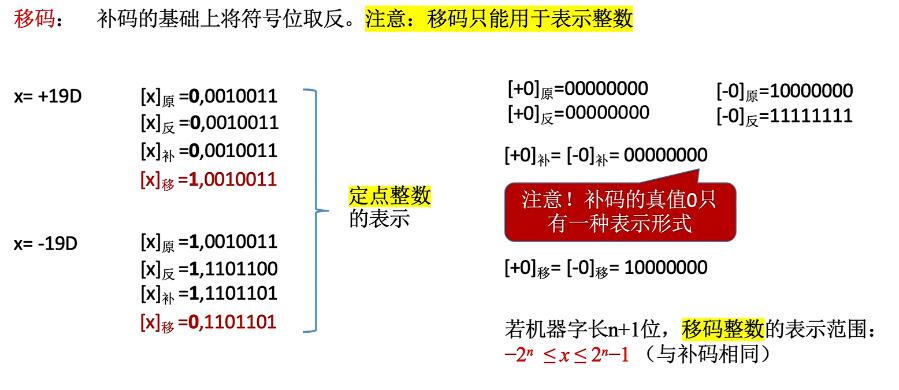 
方便计算机比较，从前到后位数哪个不是1哪个就小。各种码的作用
补码让减法变为加法，节约硬件成本，ALU无须集成减法器。
移码实现两个整数的比较大小，用硬件非常方便。移位运算
通过移位运算实现乘法和除法。 - 原码的算数移位：
符号位不变，数值位移动。
右移：高位补0，低位舍弃。舍弃的位=0则相当于除2，若舍弃的位不等0，则丢失精度。
左移：低位补0，高位舍弃。舍弃的位=0则相当于乘2，若舍弃的位不等0，则出现严重误差。 - 反码的算数移位：
正数的反码和原码一样，所以左右移位也一样。
负数的反码数值位和原码数值位相反，则：
右移：高位补1，低位舍弃。
左移：低位补1，高位舍弃。 - 补码的算数移位：
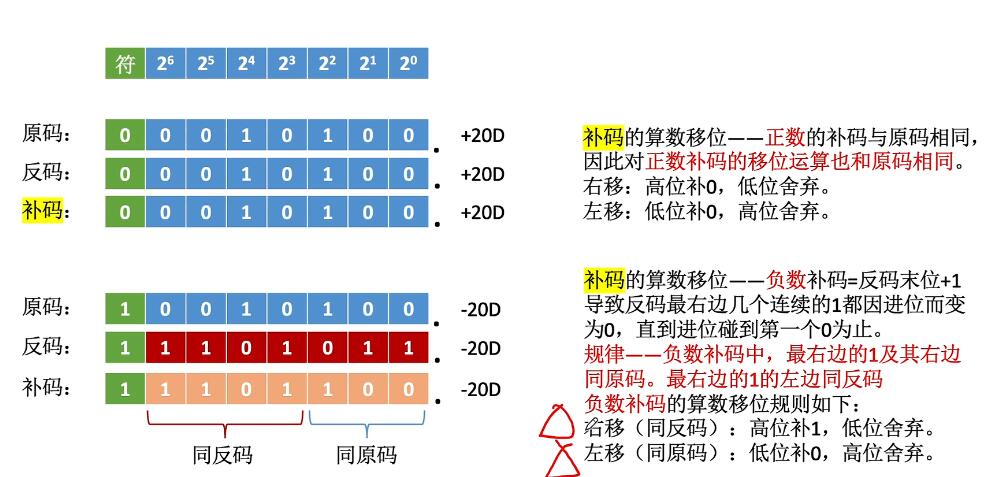
逻辑移位
单纯补充0循环移位
左右端被移出的数字放到相反的一端。
但加法溢出的一位则有一个保留进位。（进位位）加减运算
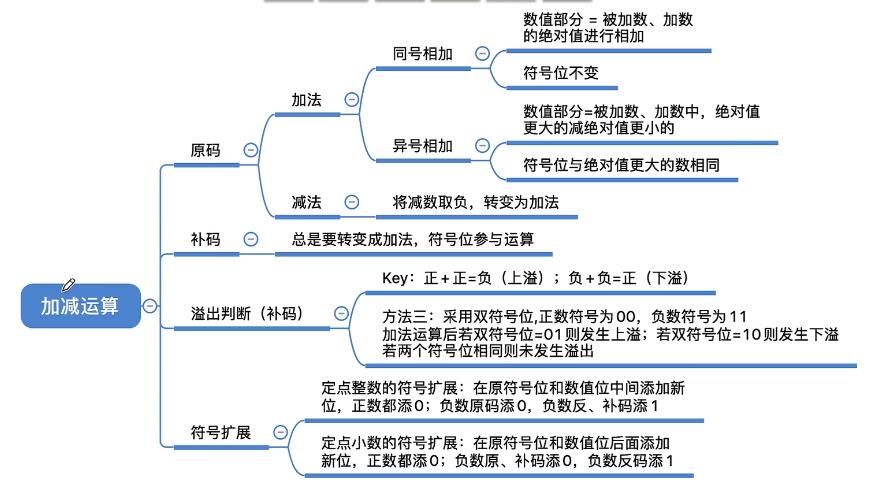
- 原码的加减：
四种加法运算：++，+-，-+，–。
四种减法运算：转化为加法。 - 补码的加减：
乘法和除法
原码和补码的乘法除法（暂不复习）强制类型转换
浮点数
定点数表示数字范围有限，但我们不能无限制增加长度。
十进制科学计数法：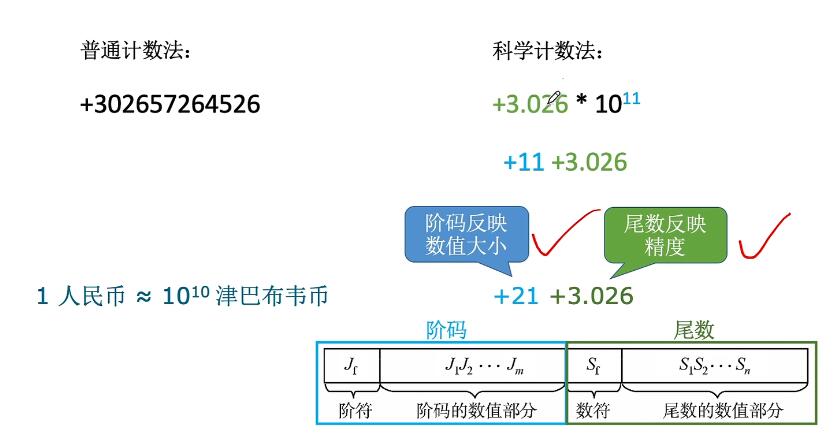
阶码E反映浮点数的表示范围及小数点的实际位置。
尾数的数值部分的位数n反映浮点数的精度。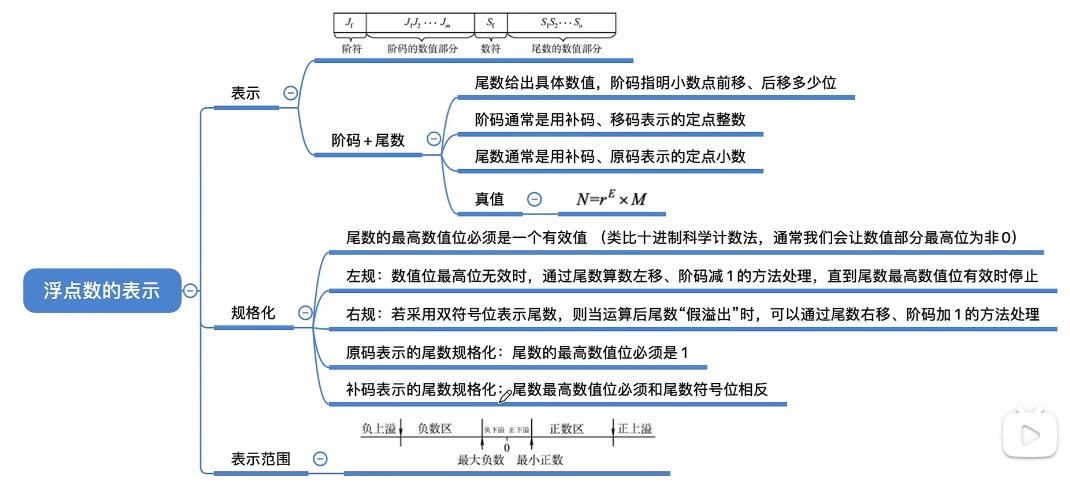
IEEE 754
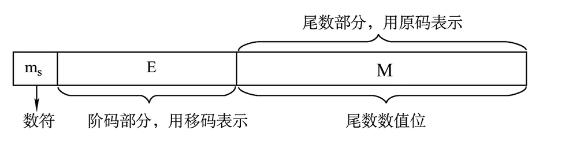浮点数标准 算数逻辑单元ALU
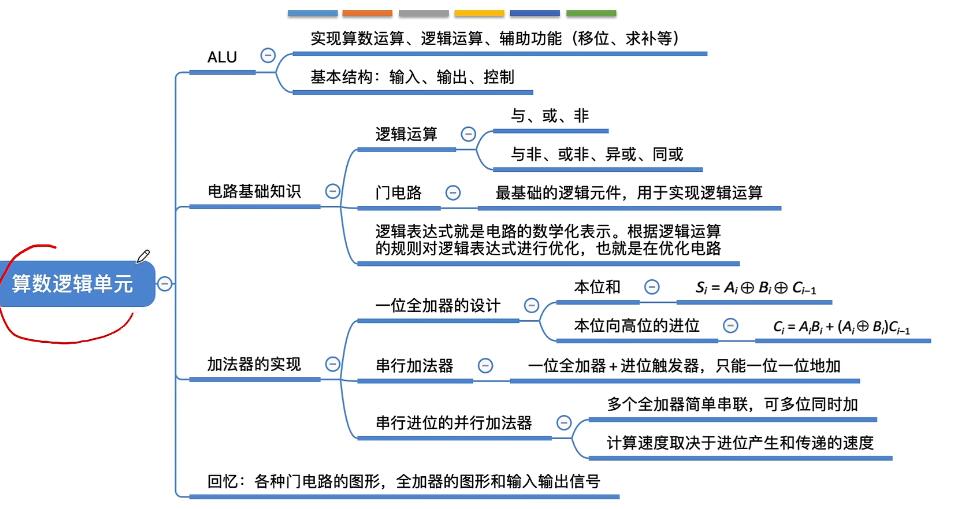
- ALU功能：算术运算（加减乘除），逻辑运算（与或非异或），辅助功能（移位，求补）。
基本结构：输入，输出，控制。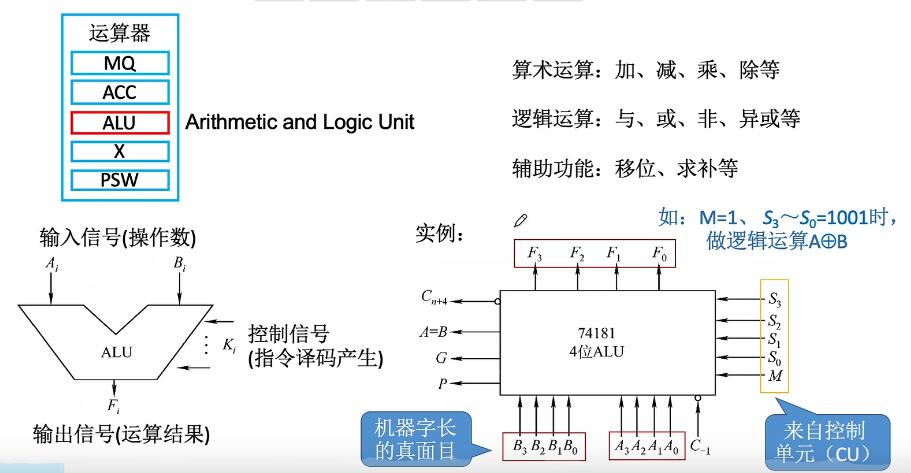
- 最基本的逻辑运算：与或非。优先级：与>或。有分配律，结合律等定义简化电路。
复合逻辑：与非，或非，异或，同或（异或的取反） - 一位全加器FA：
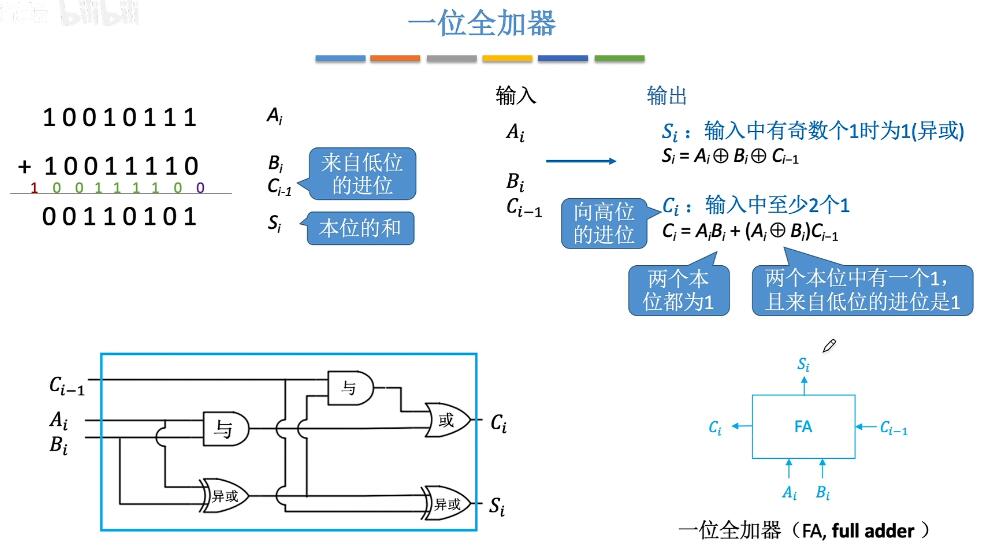
- 串行加法器：
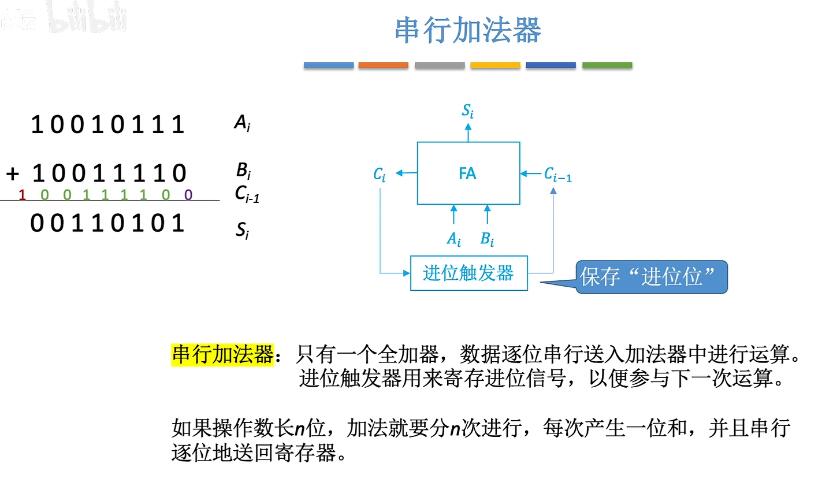
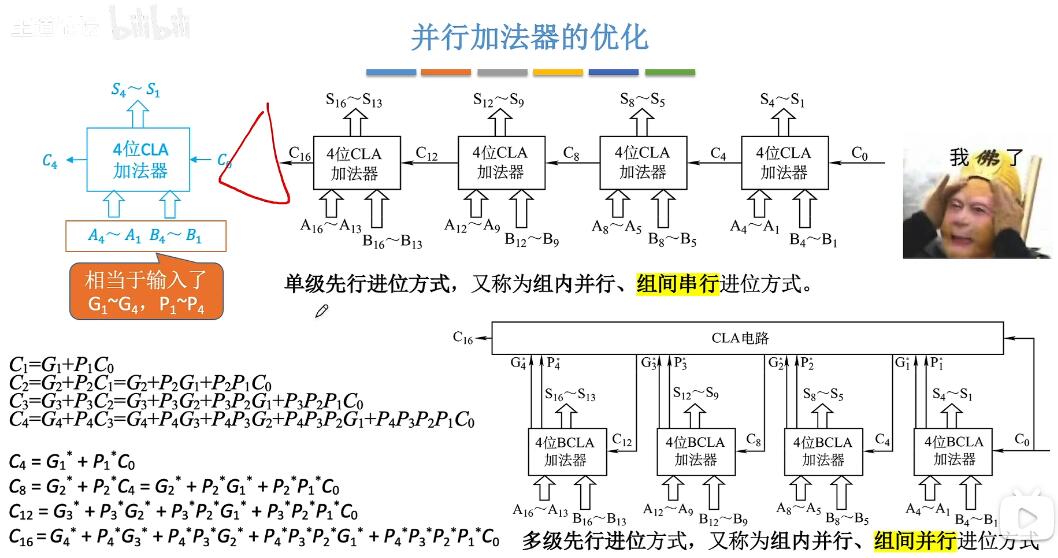
- 串行进位的并行加法器：
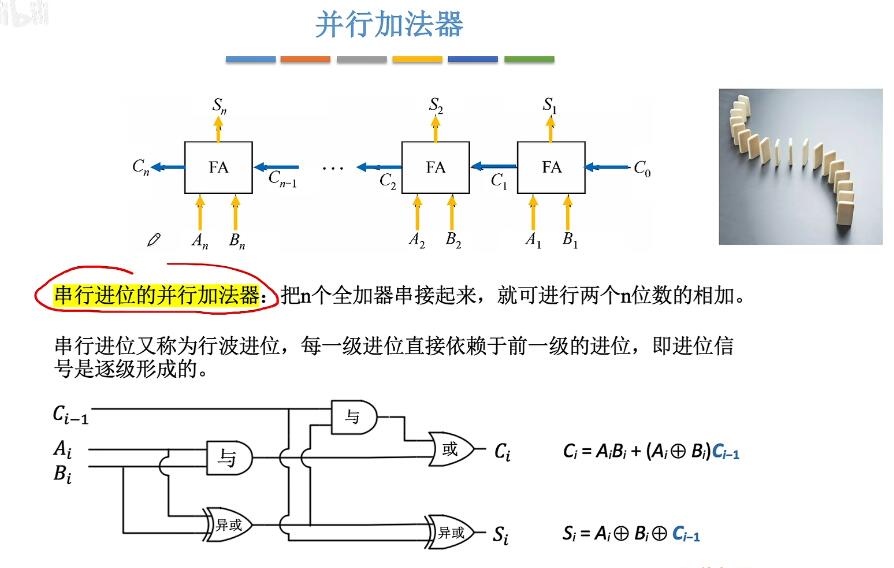一般来说是四个FA组成一个4位的计算装置，依赖于低位的进位才可以进行计算，如何更快的产生进位？
利用多个四位的计算装置再次串联
