数据结构树与二叉树
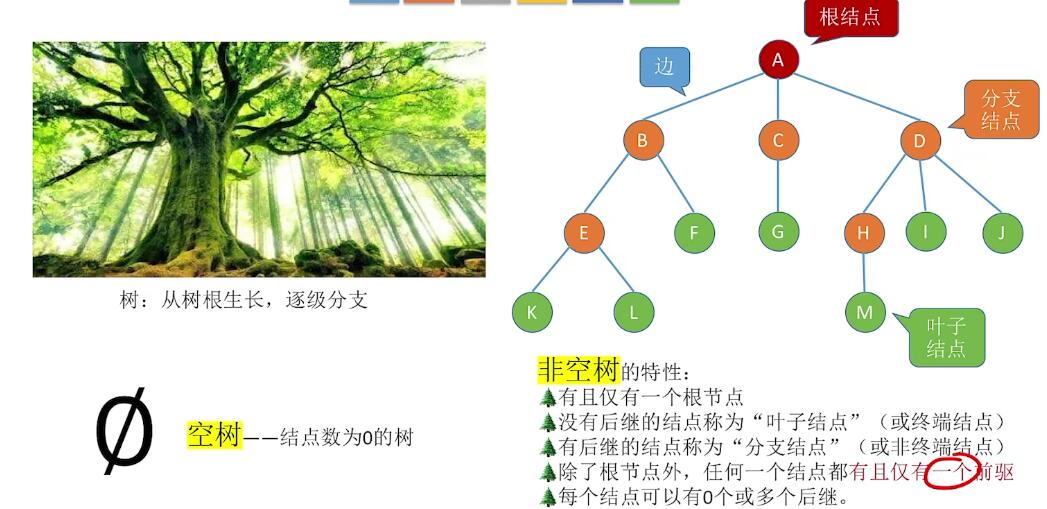
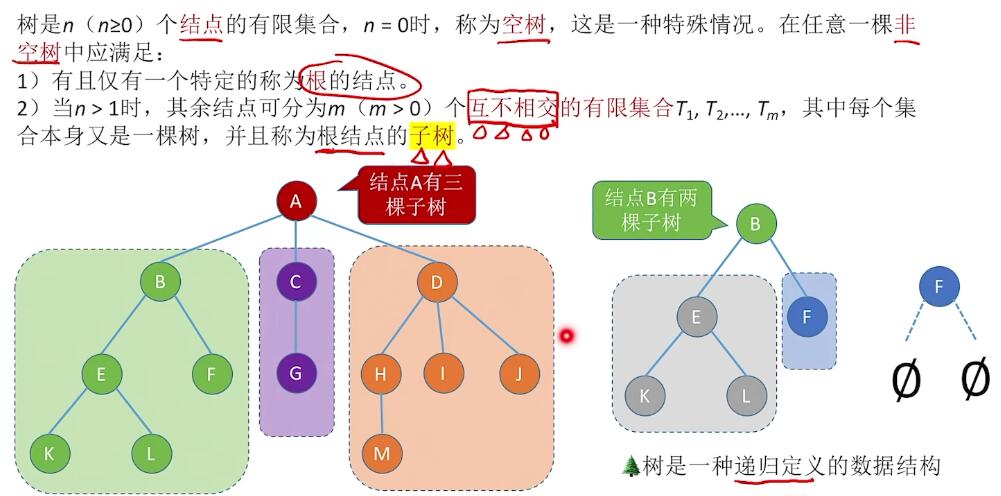
树定义

有序树vs无序树:

性质
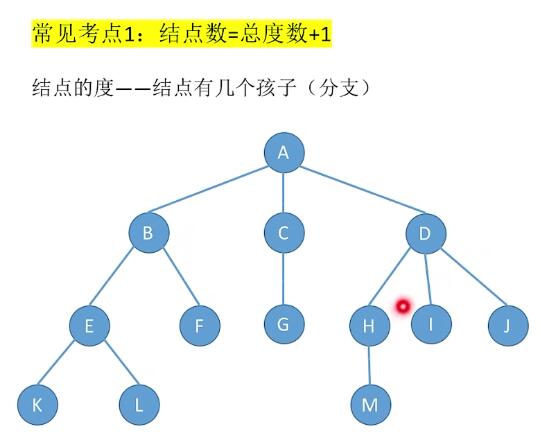
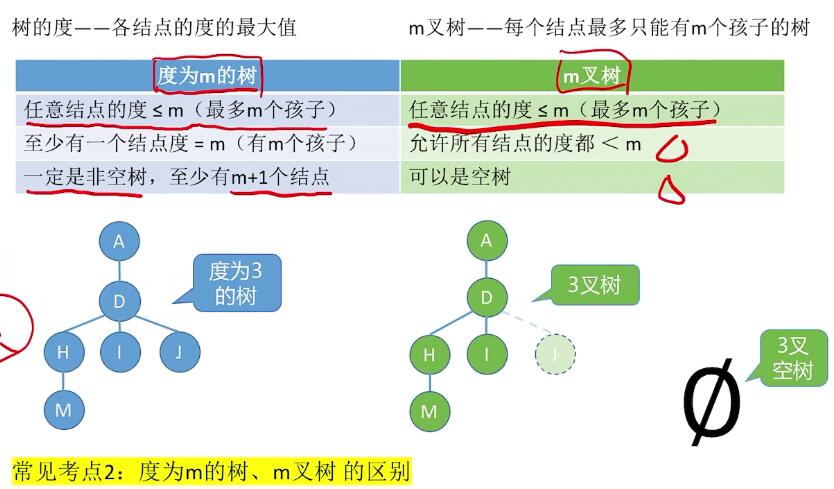
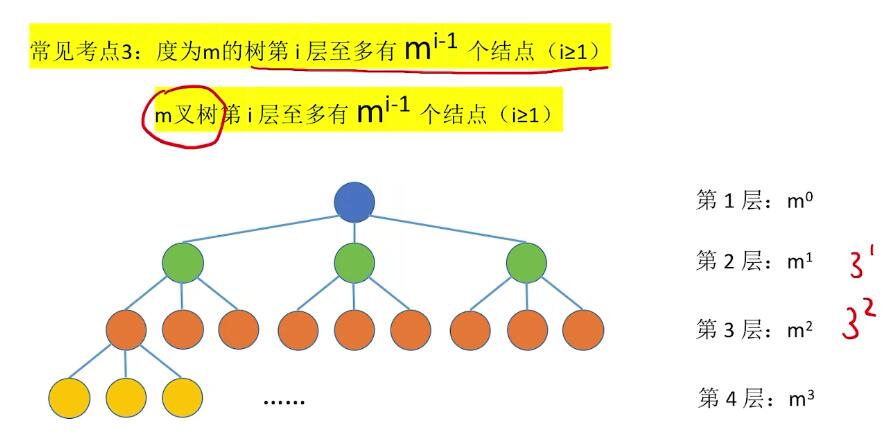
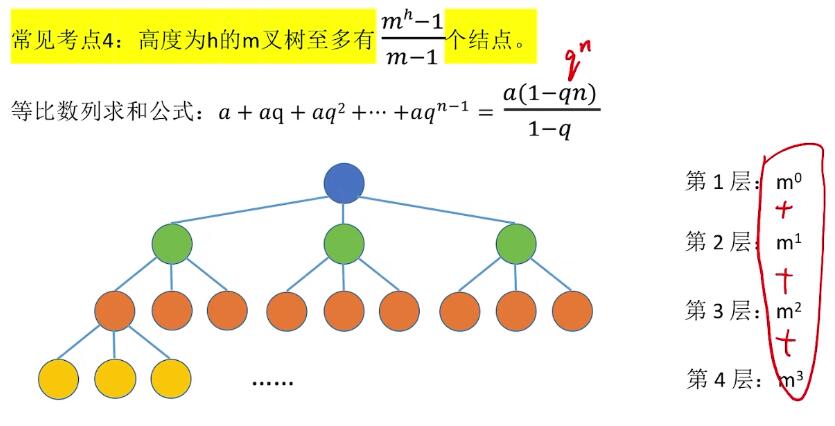


二叉树定义
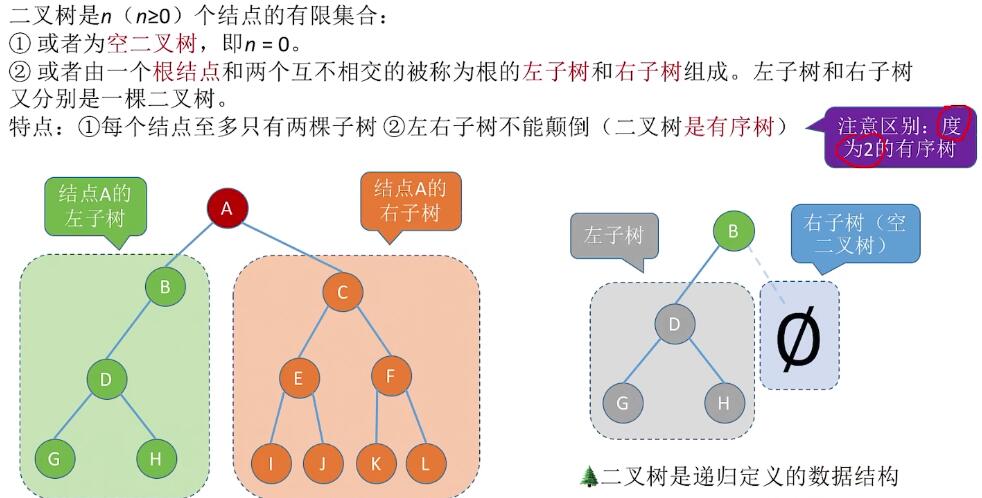
特殊二叉树:
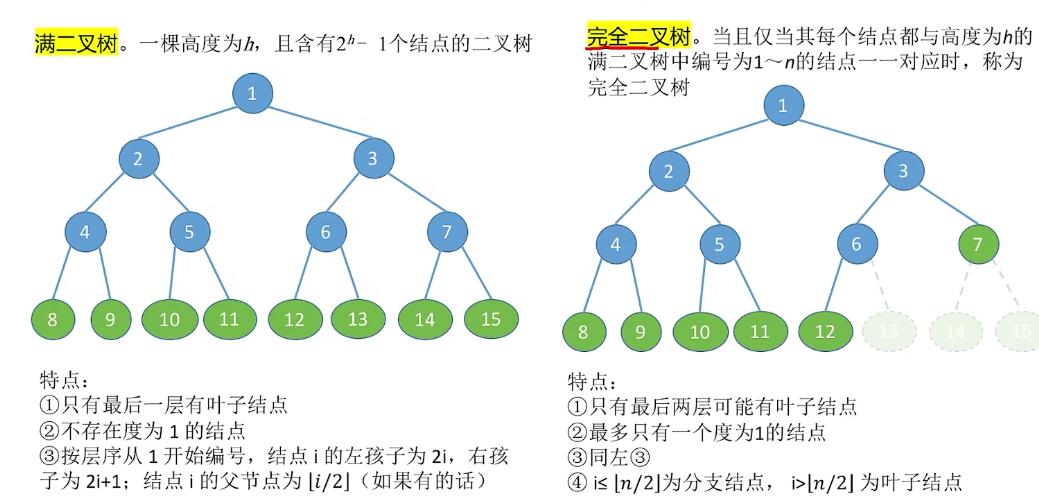
二叉树性质
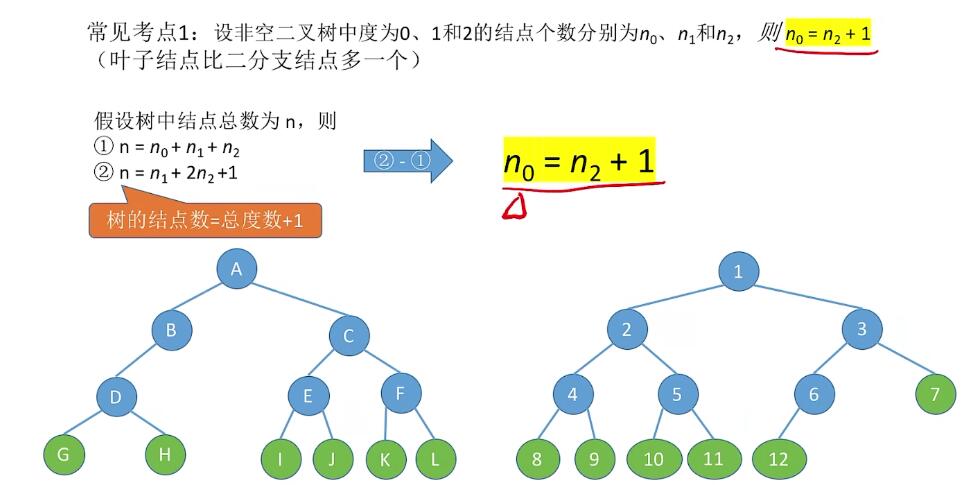
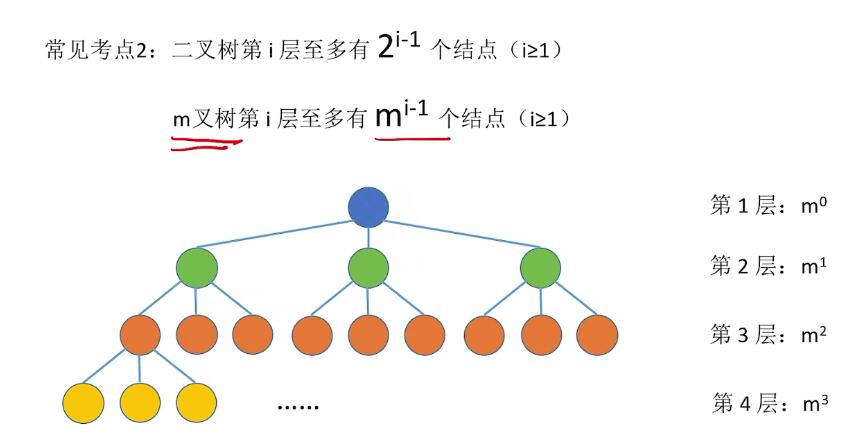
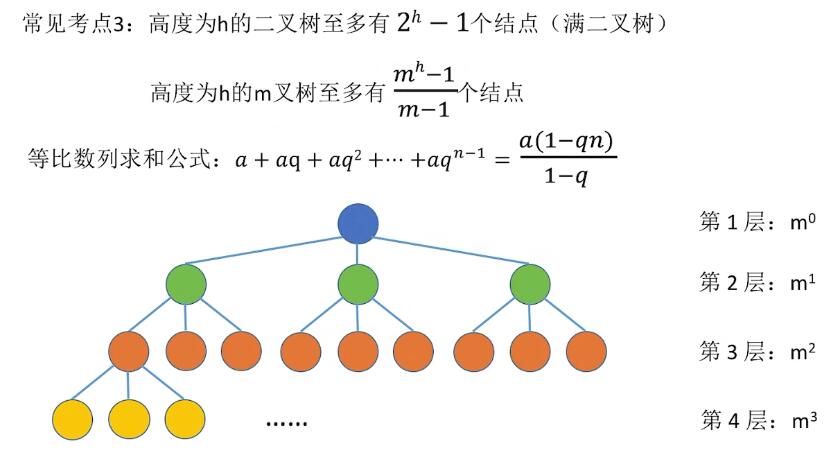
完全二叉树:
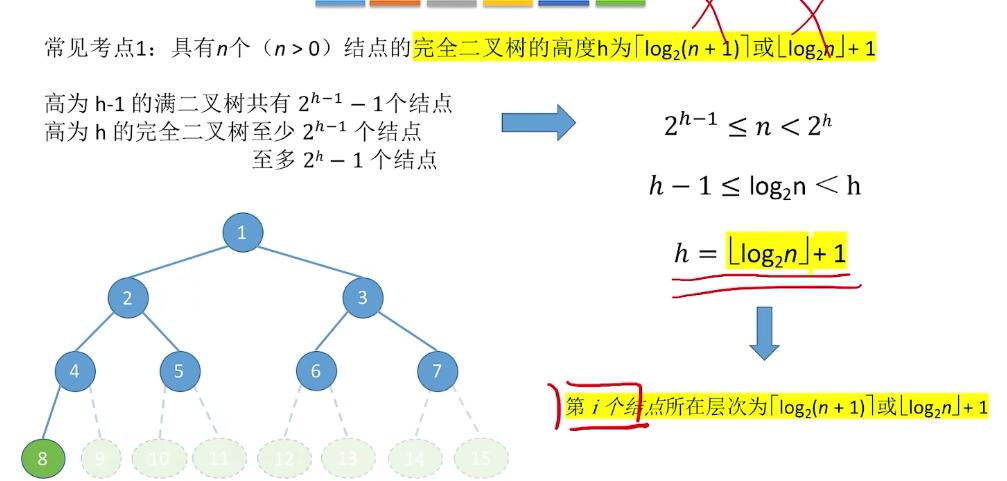
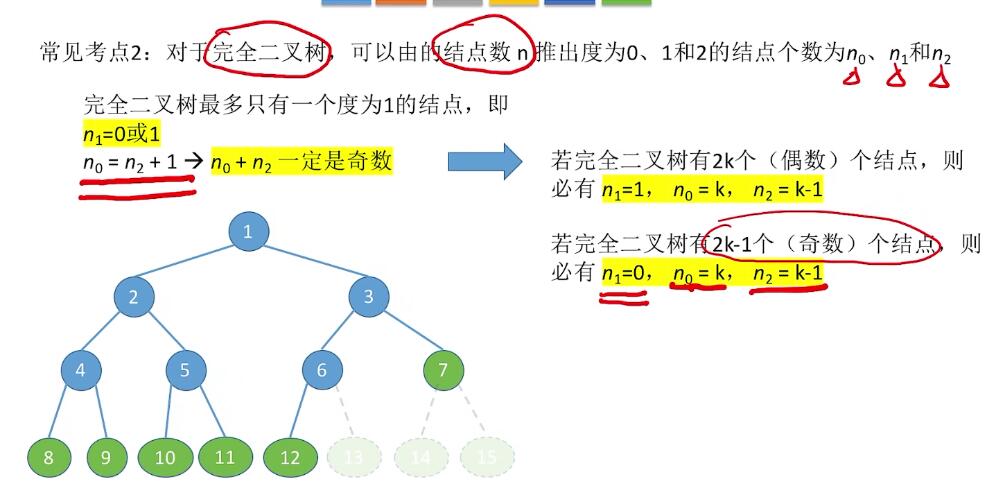
二叉树存储结构
使用数组顺序存储,只适合存储完全二叉树(非完全会浪费很多空间,i的左右孩子为2i和2i+1)
使用链式存储,n个结点二叉链表有n+1个空链表域,智能从根开始查找结点,也可以建立三叉链表(带parent指针)。
二叉树遍历
先中后序遍历,层次遍历。
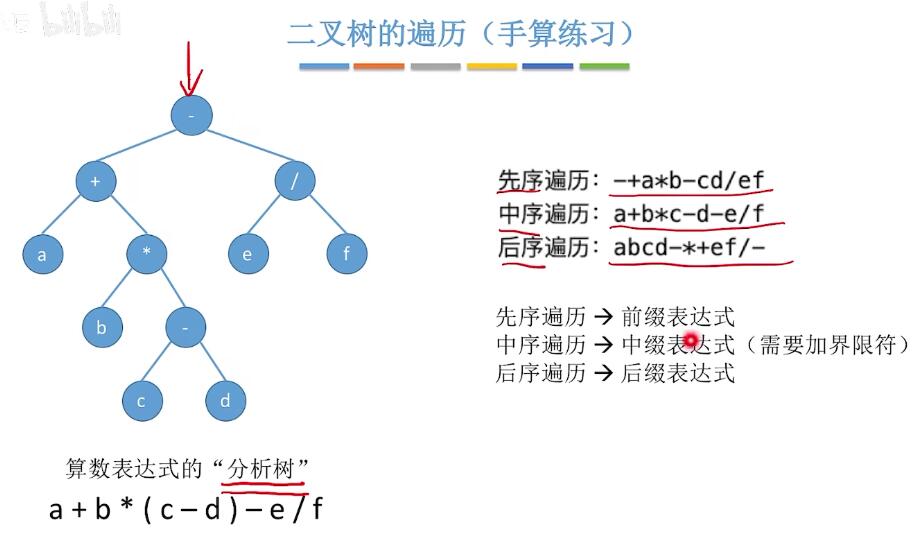
算数表达式进行三种遍历对应三种表达式:
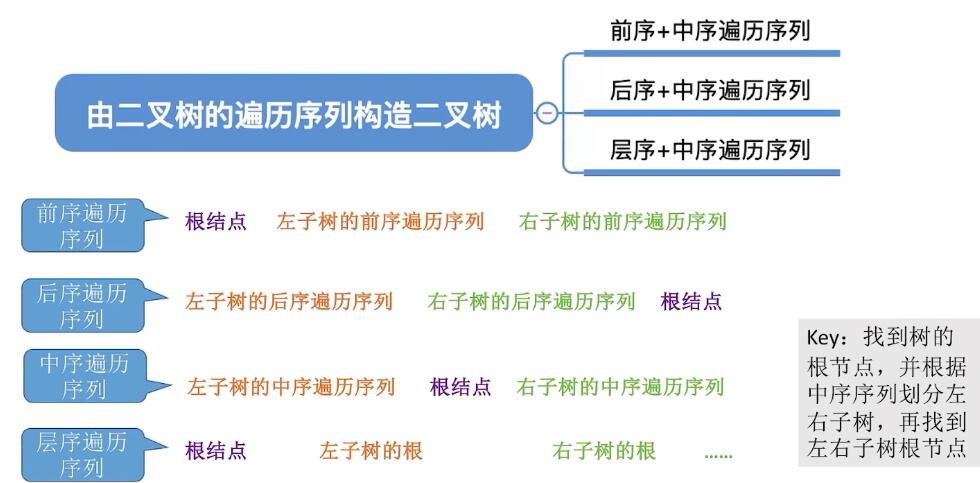
由遍历序列构造二叉树
线索二叉树(二叉链表)
所有遍历序列其实就是一个线性表,每个结点有前驱/后继。而二叉树中很难找前驱后继,所以线索二叉树就是为了查找前驱后继而创立出来。
则把n+1空链域存放其他的前驱/后继。
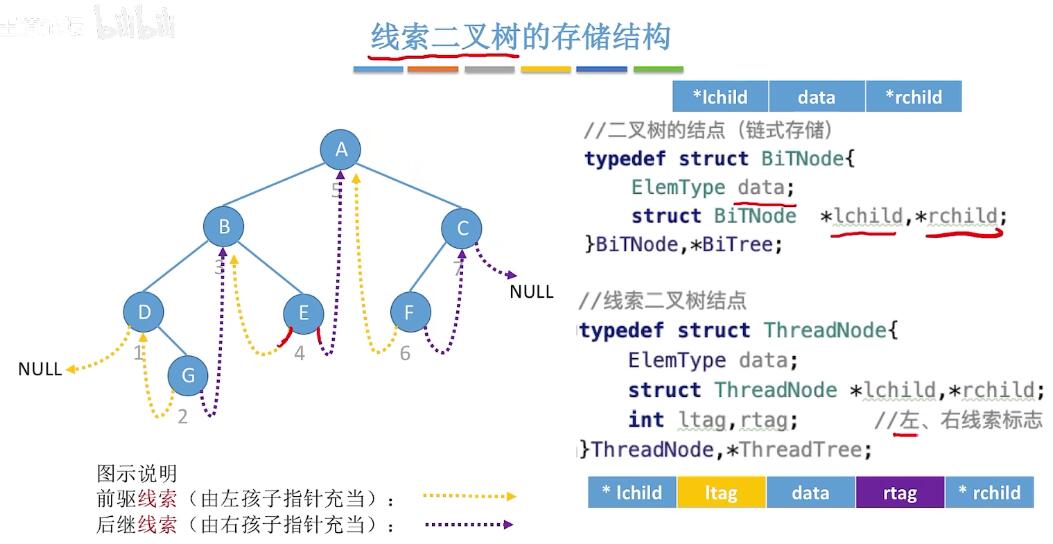
分为中序线索二叉树,先序线索二叉树,后序线索二叉树,需要对二叉树分别进行线索化。
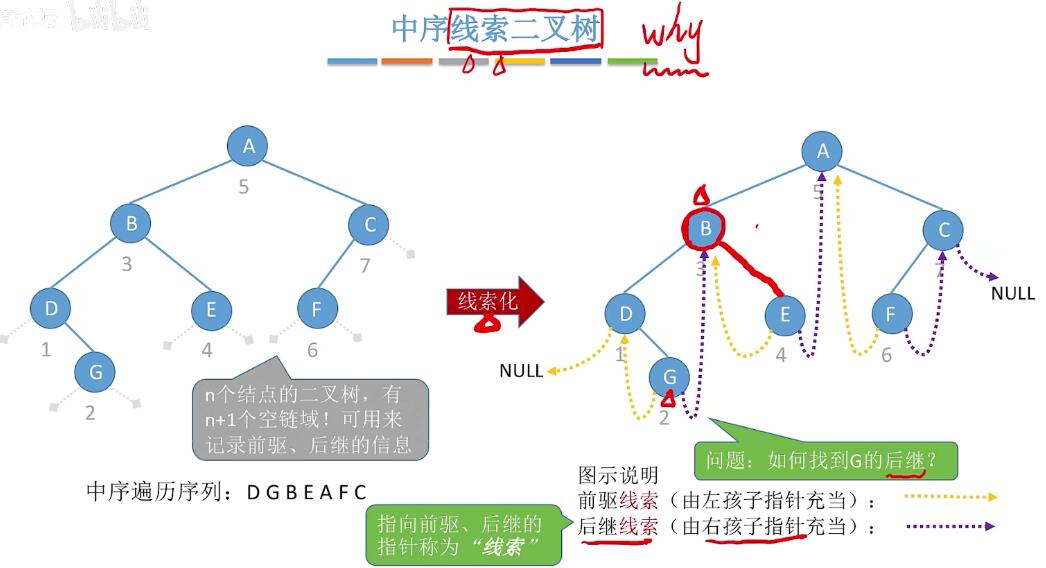
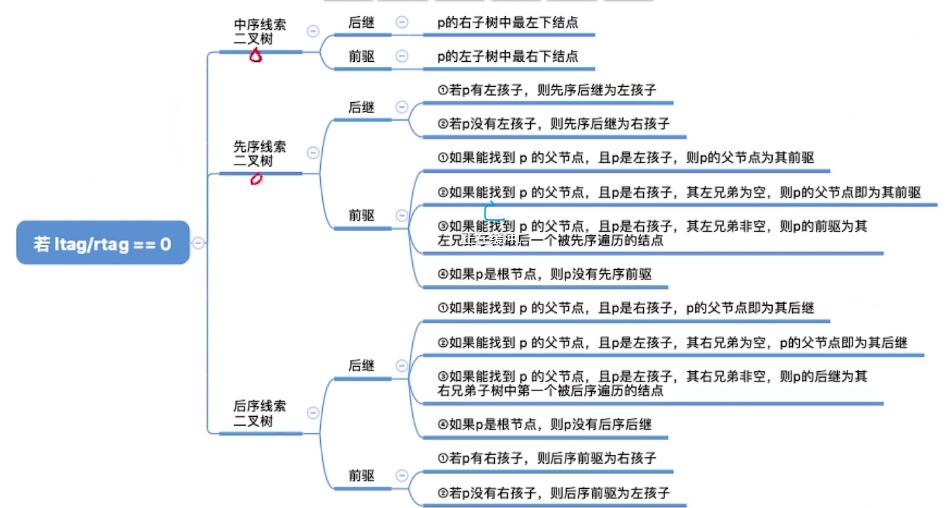
- 寻找前驱和后继:
树的存储结构
双亲表示法:找双亲简单,找孩子困难。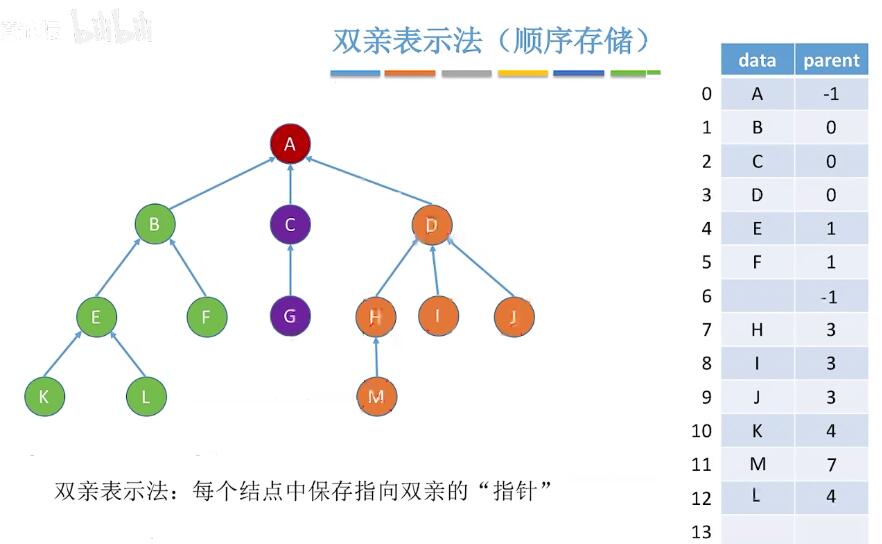 孩子表示法:找孩子简单,找双亲困难。
孩子表示法:找孩子简单,找双亲困难。 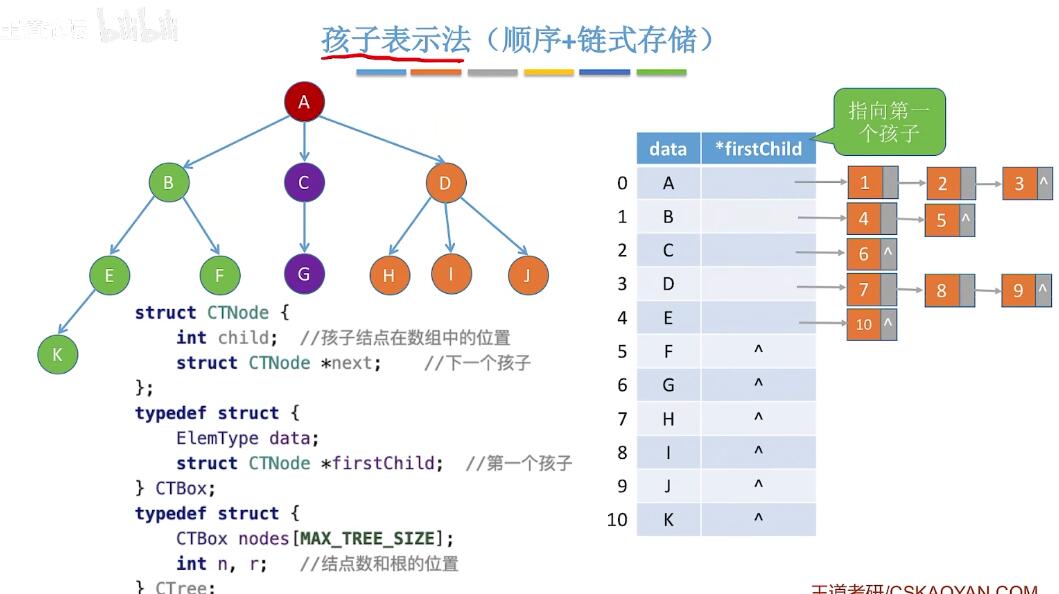 孩子兄弟表示法:(二叉树和树相互转换)
孩子兄弟表示法:(二叉树和树相互转换) 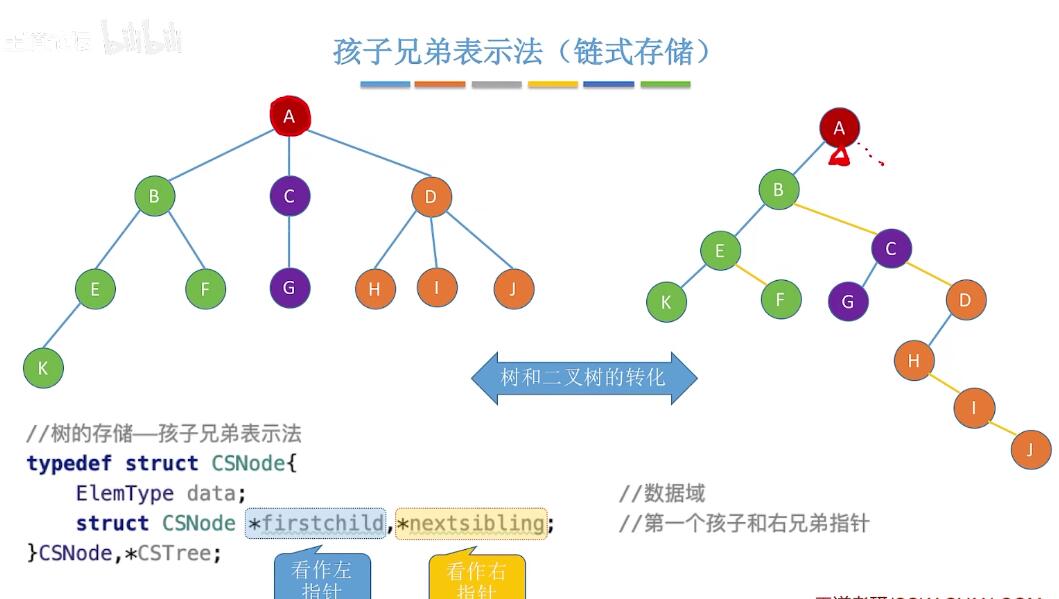 同时也可以使用这种存储结构来进行森林和二叉树的转换:
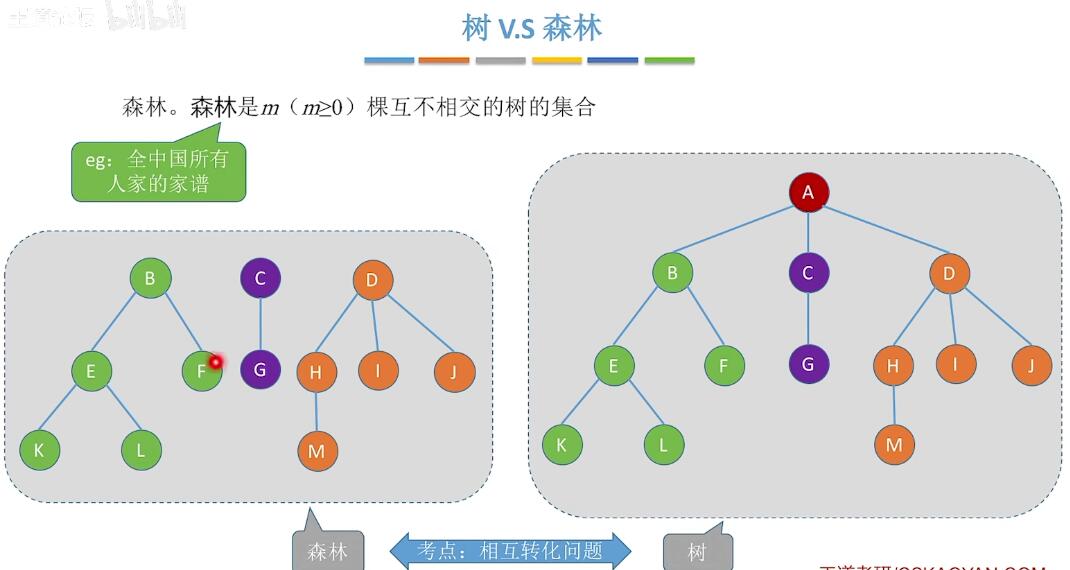
同时也可以使用这种存储结构来进行森林和二叉树的转换: 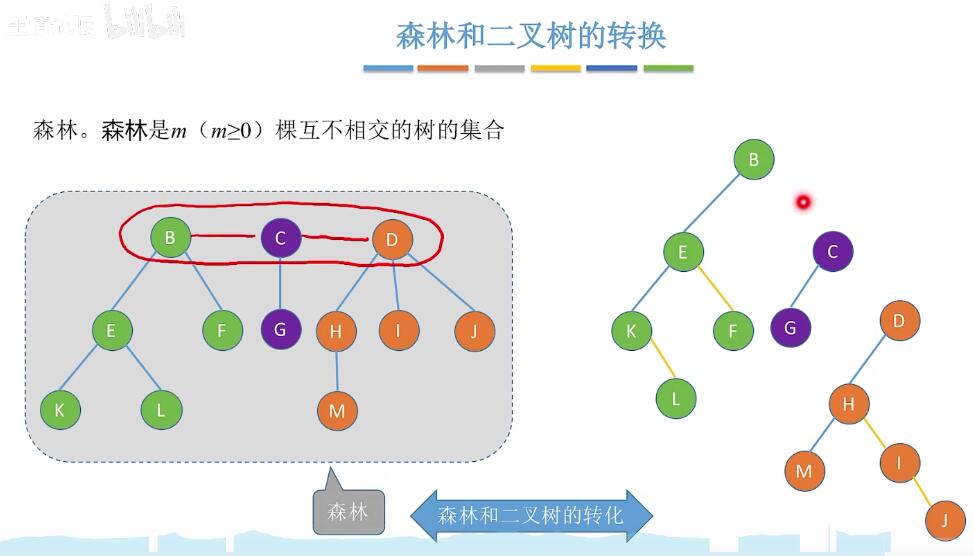
树和森林的遍历
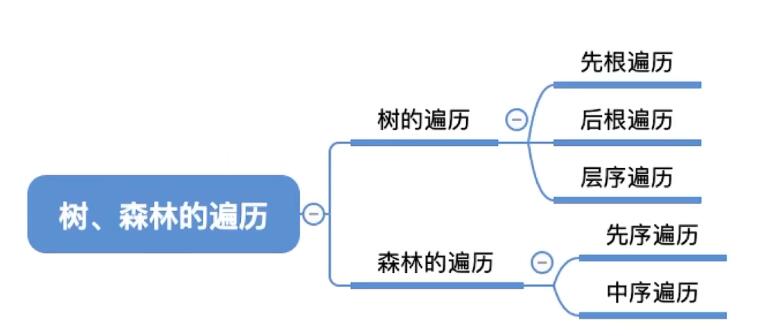 树的先根遍历:
树的先根遍历: 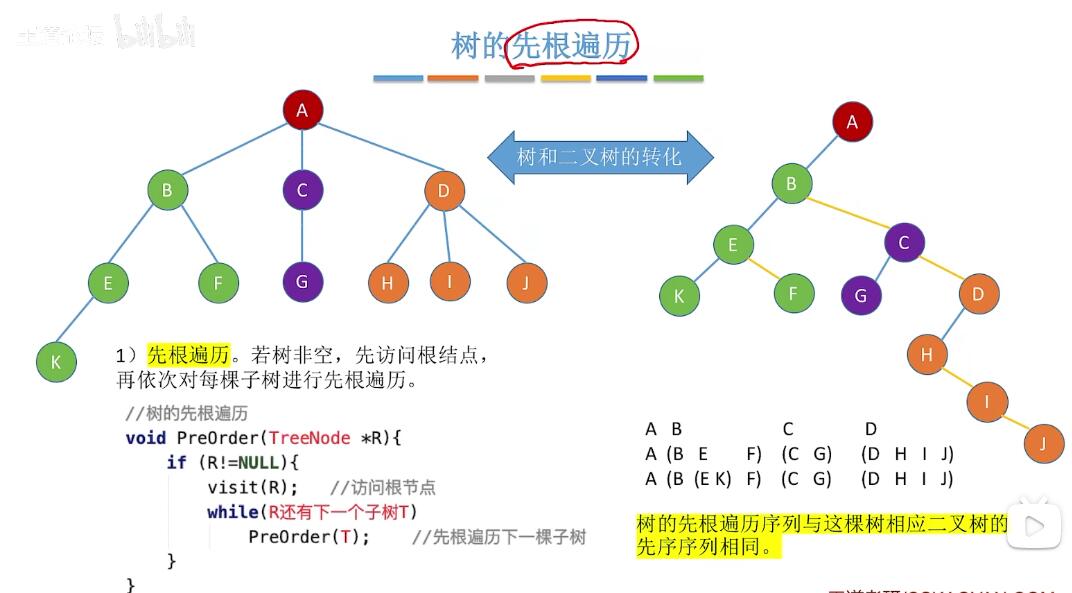 树的后根遍历:
树的后根遍历: 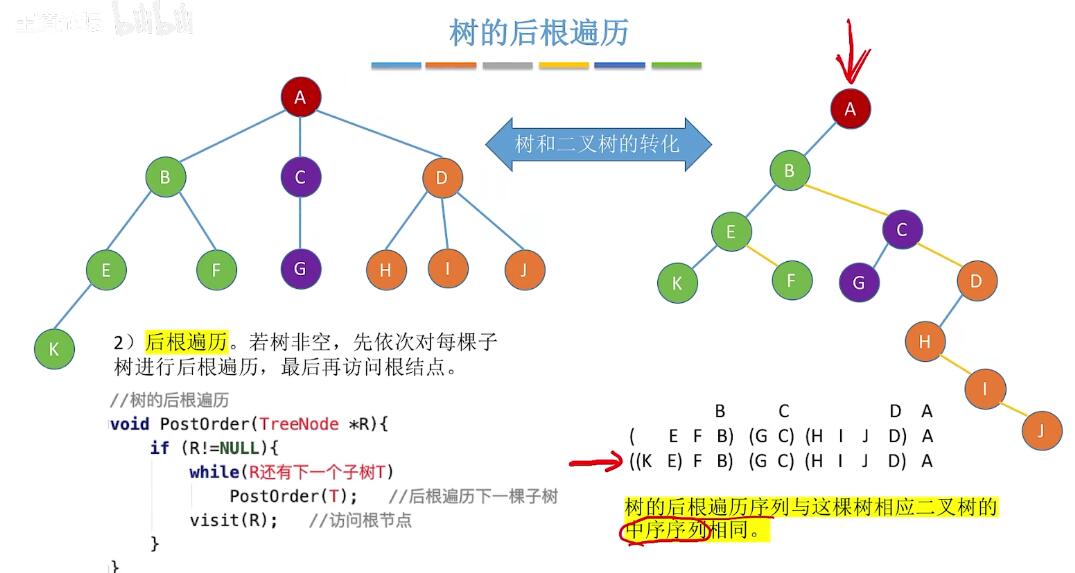 树的层次遍历:
树的层次遍历: 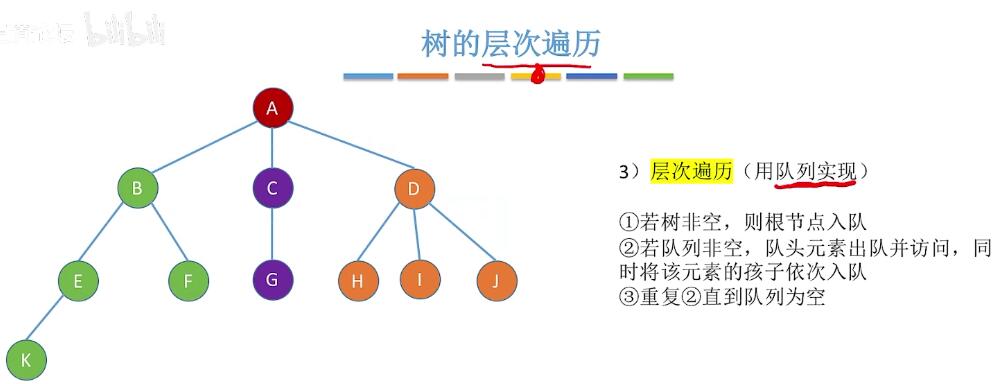 森林的先序遍历:
森林的先序遍历: 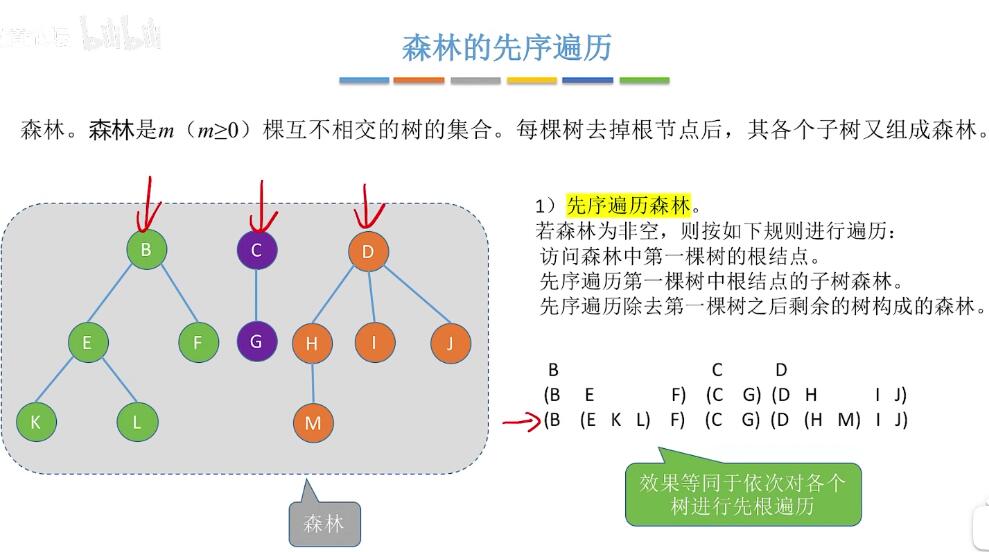 (效果相当于对每个子树先根遍历,把森林转化为二叉树相当于二叉树的先序遍历)
(效果相当于对每个子树先根遍历,把森林转化为二叉树相当于二叉树的先序遍历)
森林的中序遍历: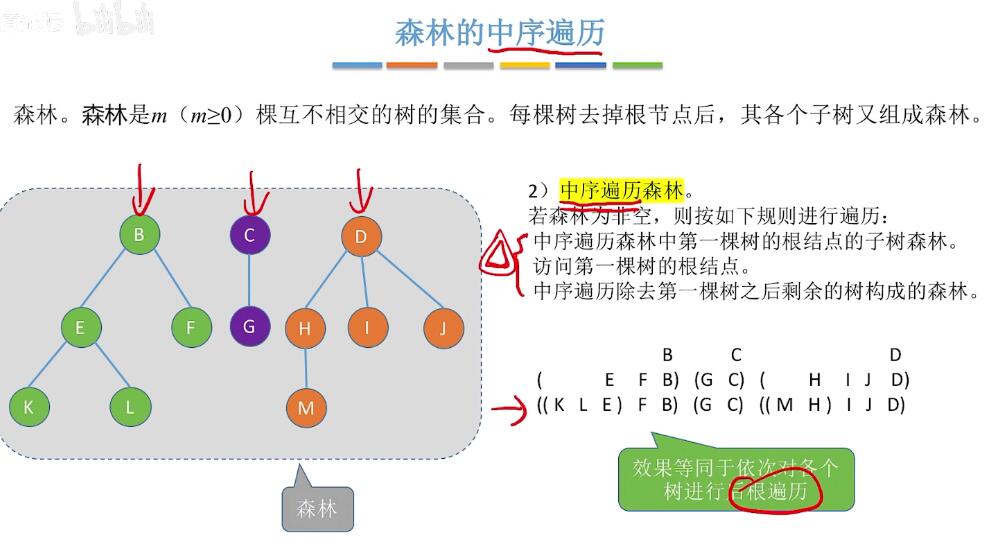 (效果相当于对每个子树后根遍历,把森林转化为二叉树相当于二叉树的中序遍历)
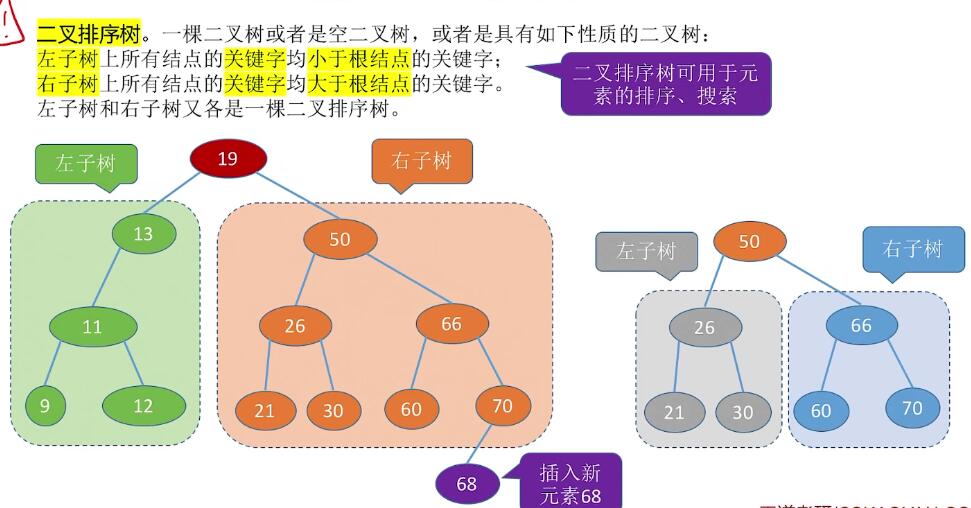
(效果相当于对每个子树后根遍历,把森林转化为二叉树相当于二叉树的中序遍历)二叉排序树
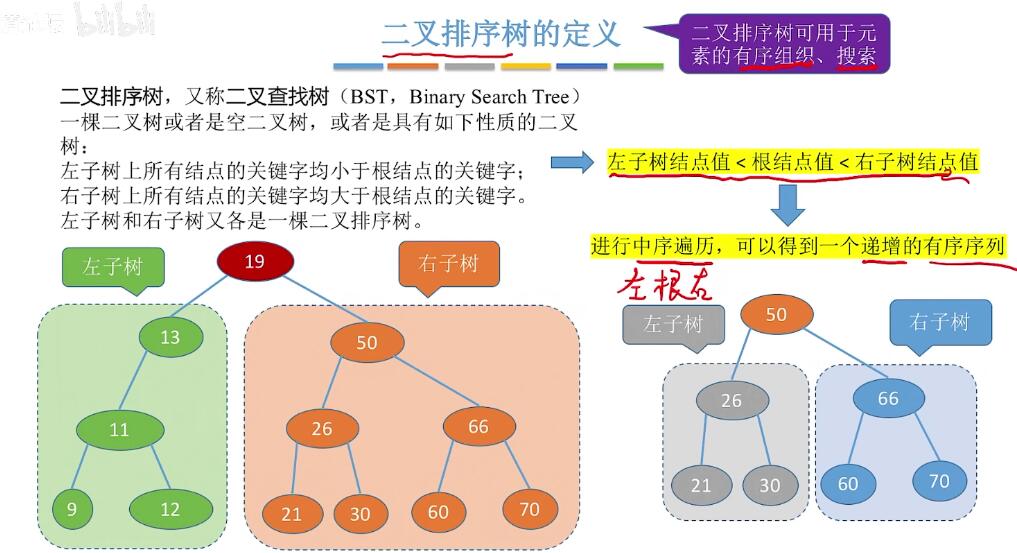 需要懂得BST的查找,插入,删除,构造(不同的关键字序列可能得到同款BST,也可能不同BST)。
需要懂得BST的查找,插入,删除,构造(不同的关键字序列可能得到同款BST,也可能不同BST)。
删除:①叶子结点直接删除。②只有左子树/右子树,直接替代。③:左右子树都有,利用前驱/后继来替代,如图: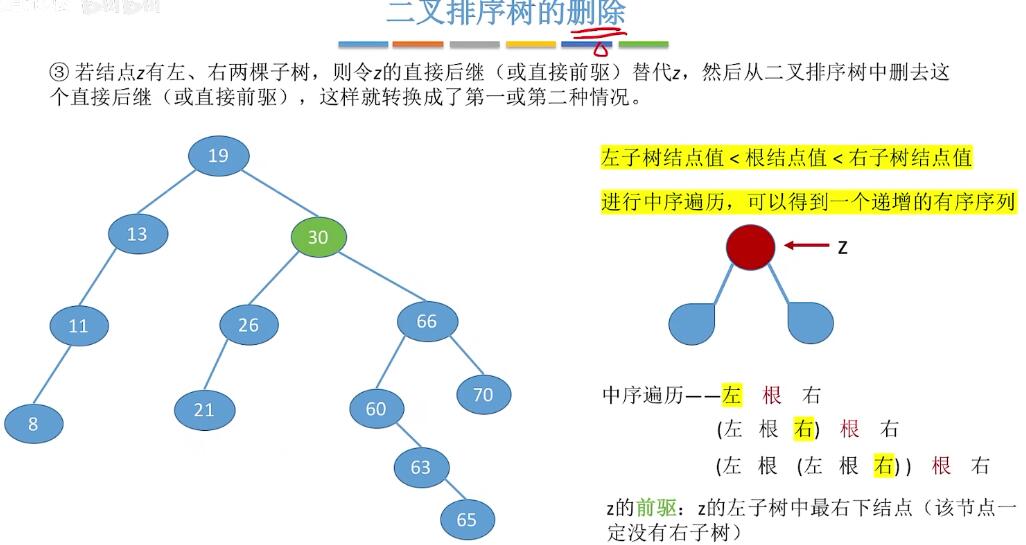
- 查找效率:
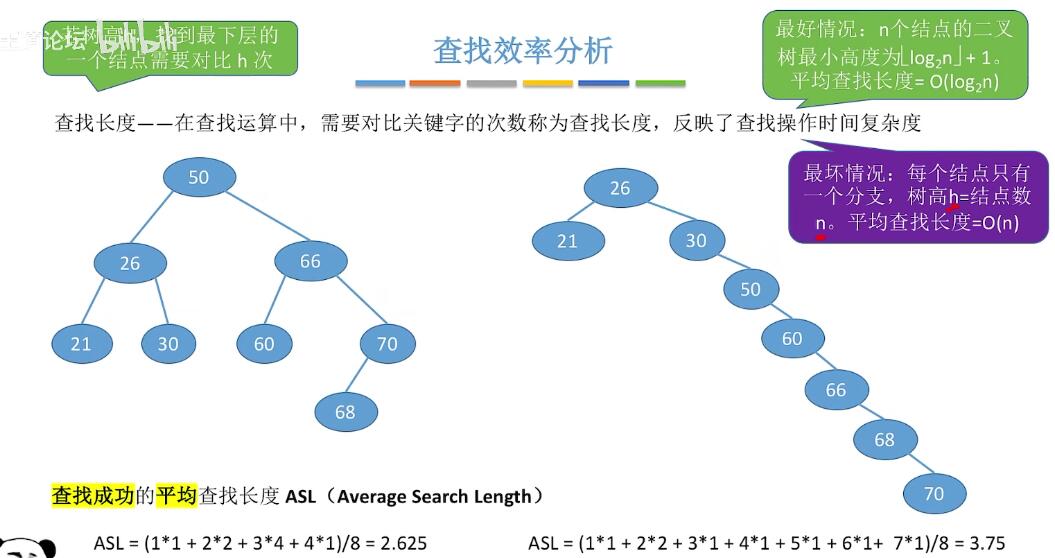
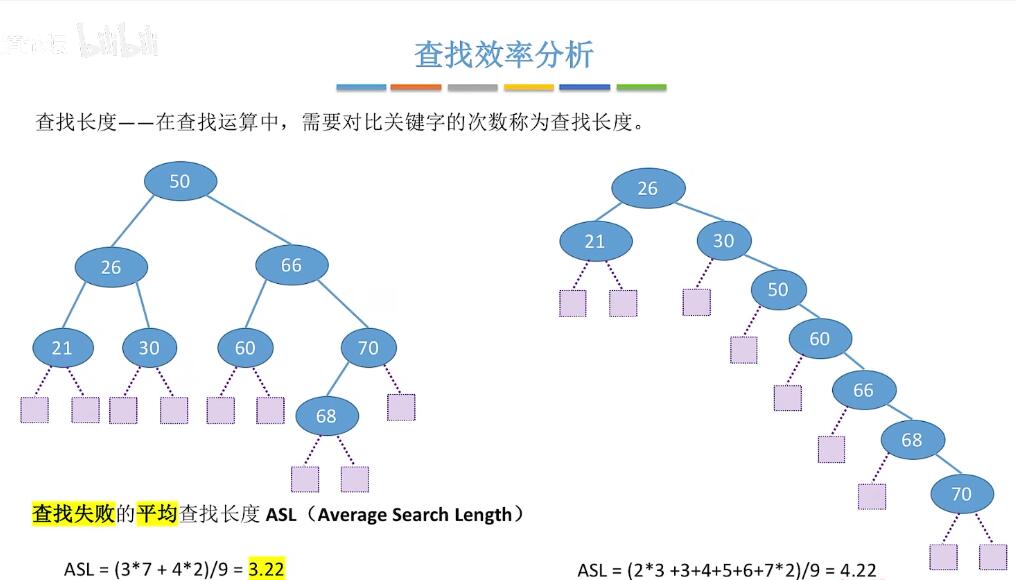 尽量让左右子树保持平衡
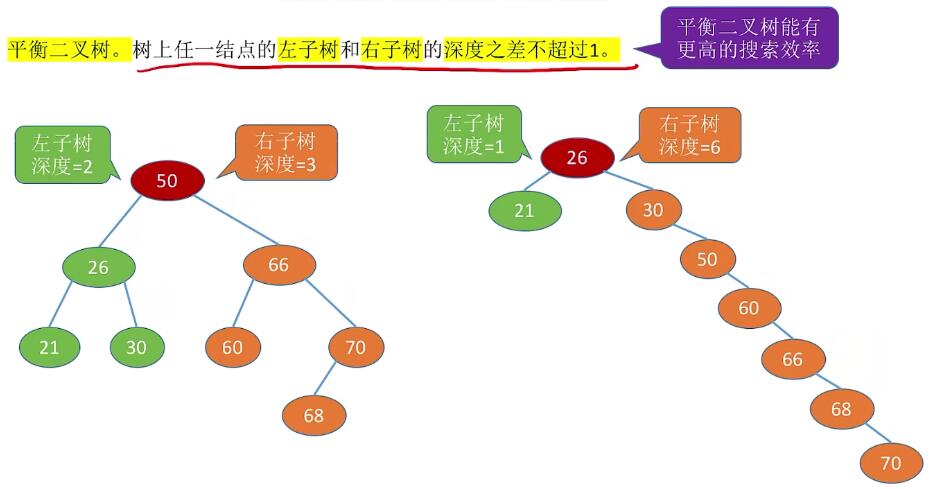
尽量让左右子树保持平衡平衡二叉树
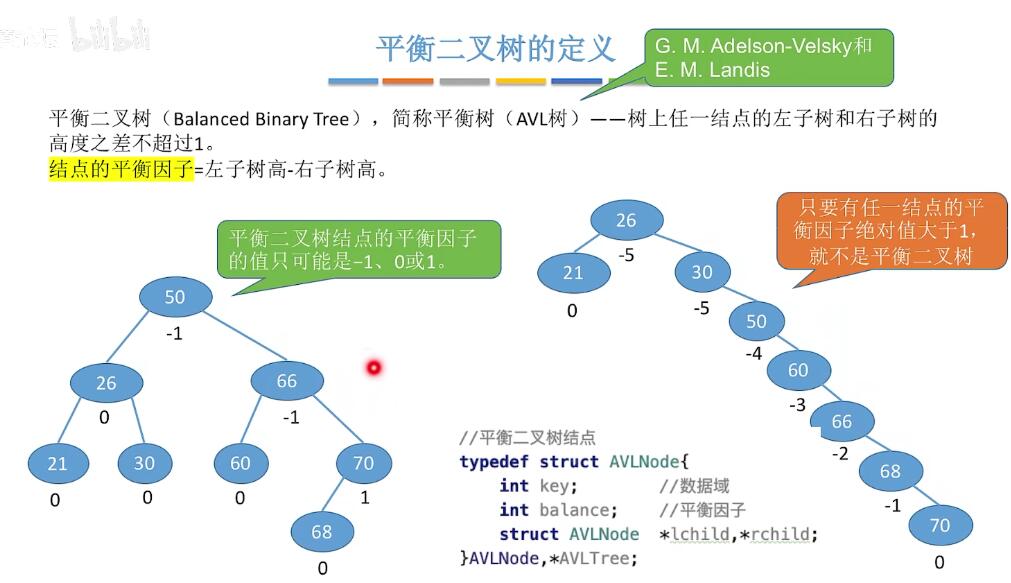 插入结点可能会导致不平衡:
插入结点可能会导致不平衡: 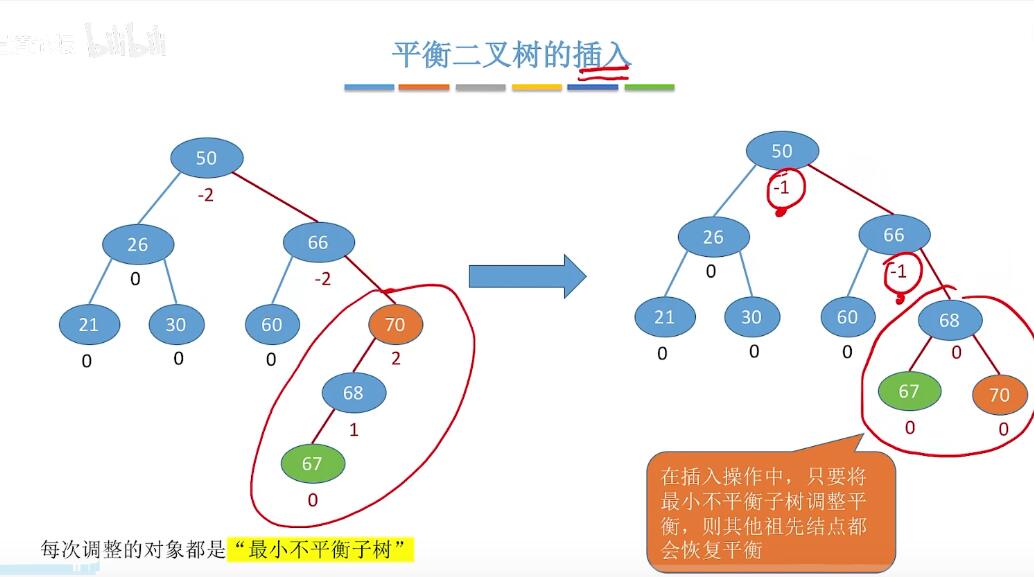 调整的四种策略:
调整的四种策略: 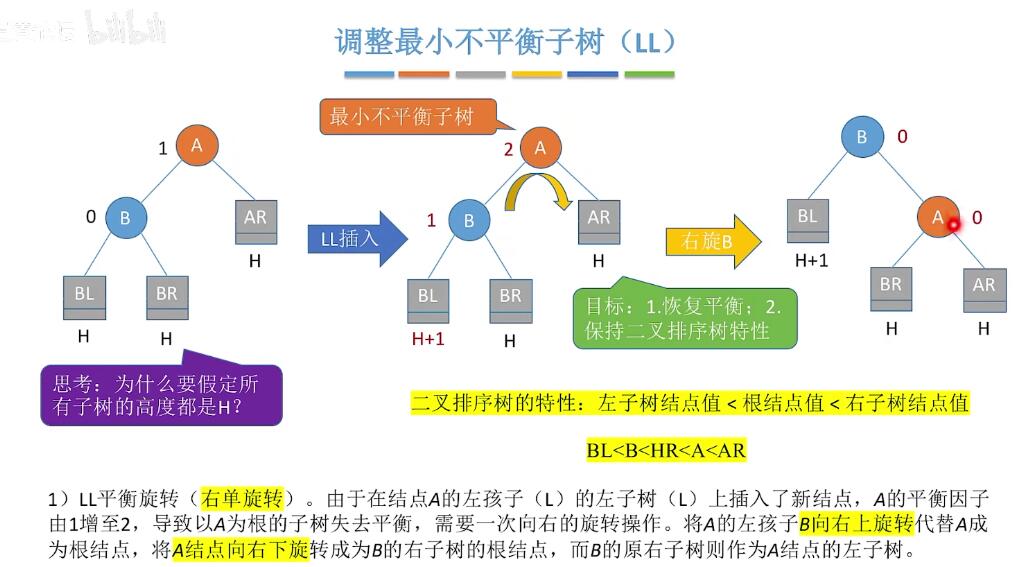
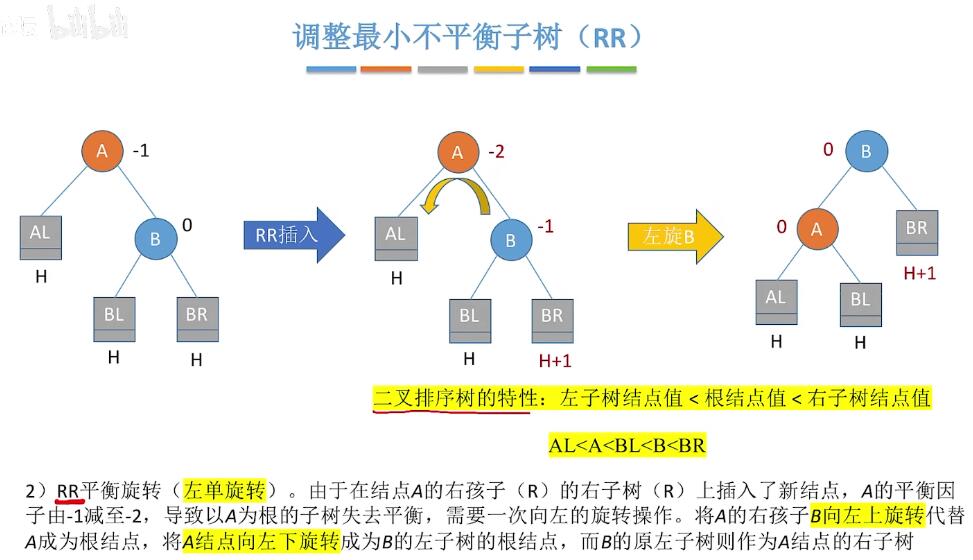
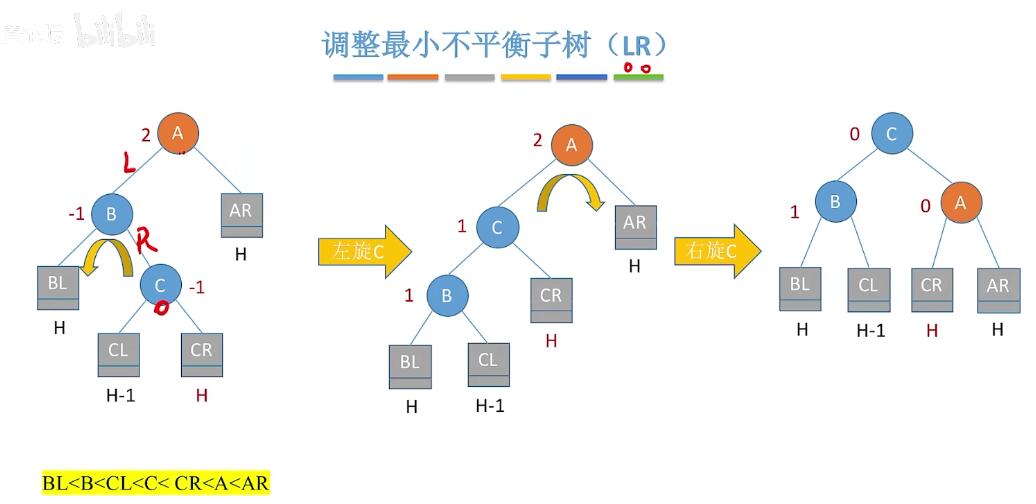
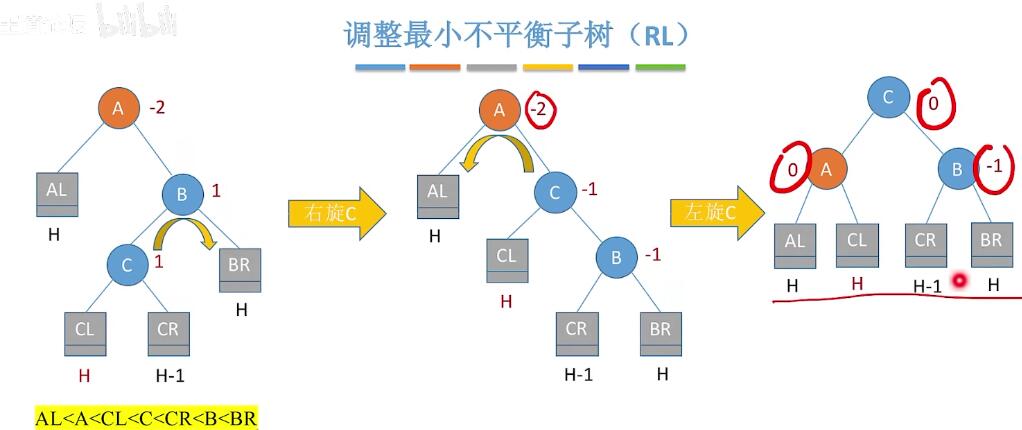 查找效率:
查找效率: 
红黑树
红黑树是一种自平衡二叉排序树,它属于平衡树,但是却没有平衡二叉树那么“平衡”。
红黑树的规则:
规则1: 每个节点不是黑色就是红色
规则2: 根节点为黑色
规则3:红色节点的父节点和子节点不能为红色
规则4:所有的叶子节点都是黑色(空节点视为叶子节点NIL)
规则5:每个节点到叶子节点的每个路径黑色节点的个数相等。 - 跟AVL区别:
平衡二叉树的左右子树的高度差绝对值不超过1,但是红黑树在某些时刻可能会超过1,只要符合红黑树的五个条件即可。
二叉树只要不平衡就会进行旋转,而红黑树不符合规则时,有些情况只用改变颜色不用旋转,就能达到平衡。 - 通过改变颜色/旋转来维持红黑树的平衡。
哈夫曼树
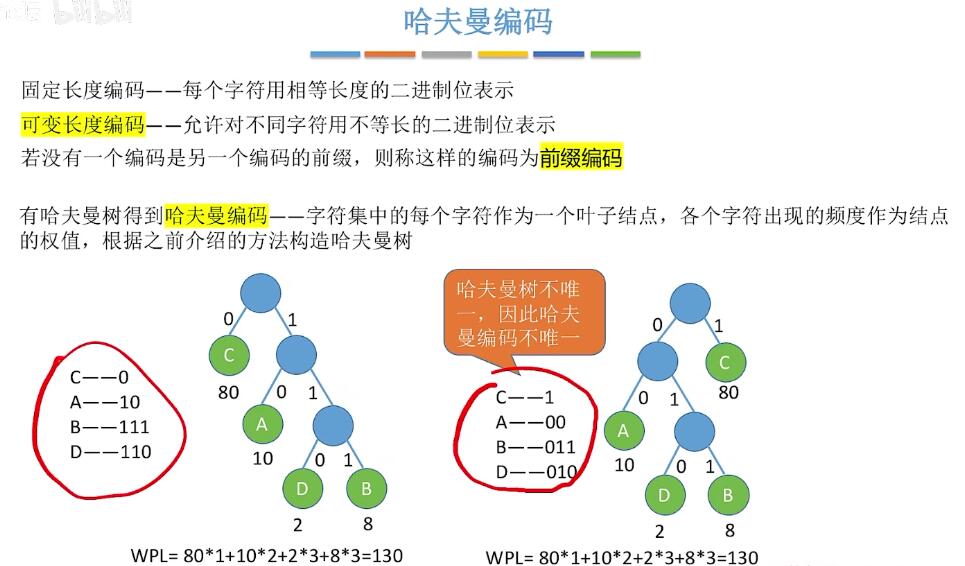
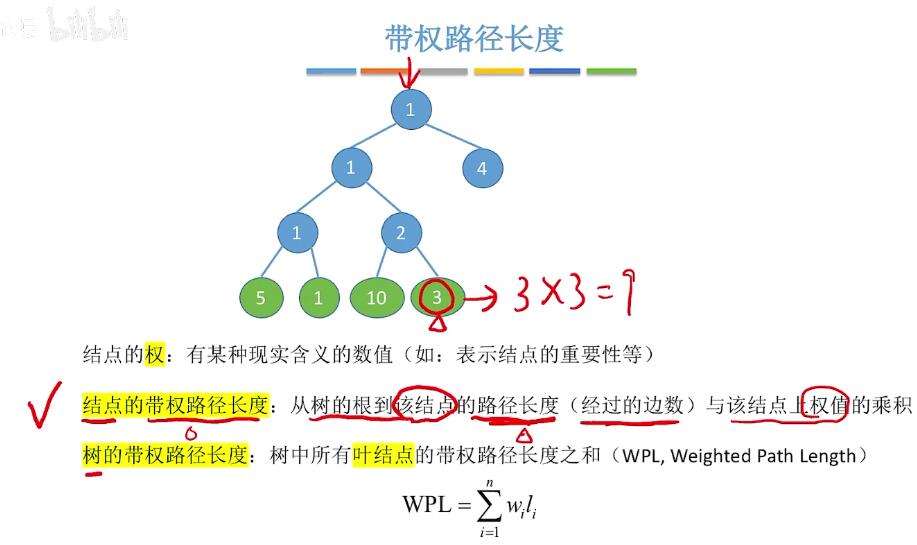 在含有n个带权叶结点的二叉树中,带权路径长度WPL最小的二叉树为哈夫曼树,也叫最优二叉树。
在含有n个带权叶结点的二叉树中,带权路径长度WPL最小的二叉树为哈夫曼树,也叫最优二叉树。 - 构造:
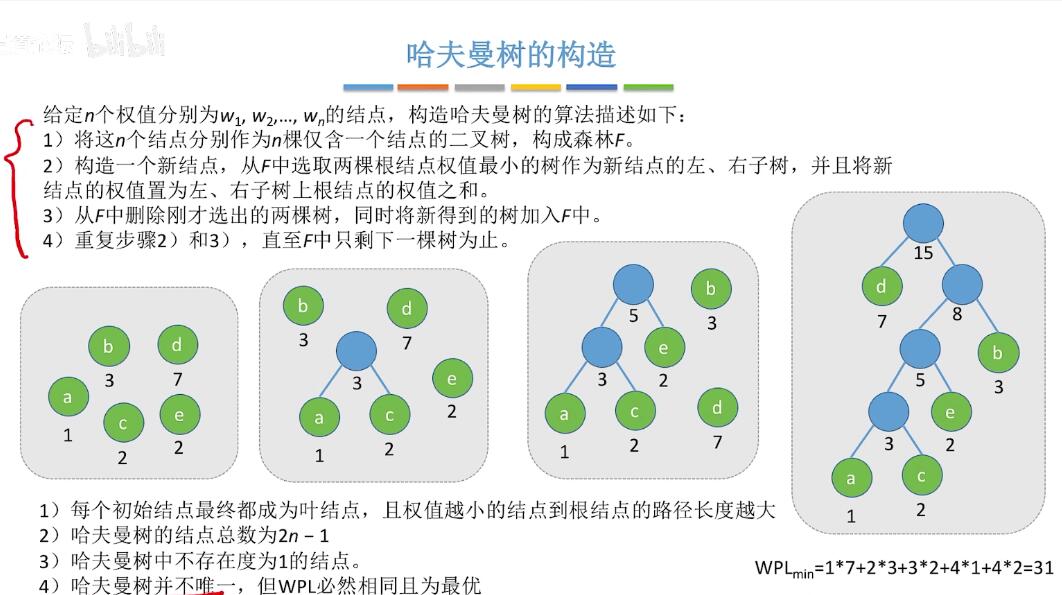
- 哈夫曼编码: